視野角の変換式でアスペクト比の比率を用いましたが今回はモニターディスタンスを係数として利用することにします。また画面上のズーム倍率で視野角を変換し腰だめ視野角からADS視野角を求めます。
前の記事:FPSとFOV② 異なるアスペクト比に視野角を変換
タンジェントで整理する
| $$ \mbox{[出力fov]}=atan\left( \frac{\mbox{[変換先アス比]}}{\mbox{[変換元アス比]}} tan\left( \mbox{ [入力fov]}\frac{\pi}{360}\right) \right) \frac{360}{\pi} $$ |
アスペクト比による視野角の変換式はタンジェントで表された式でした。

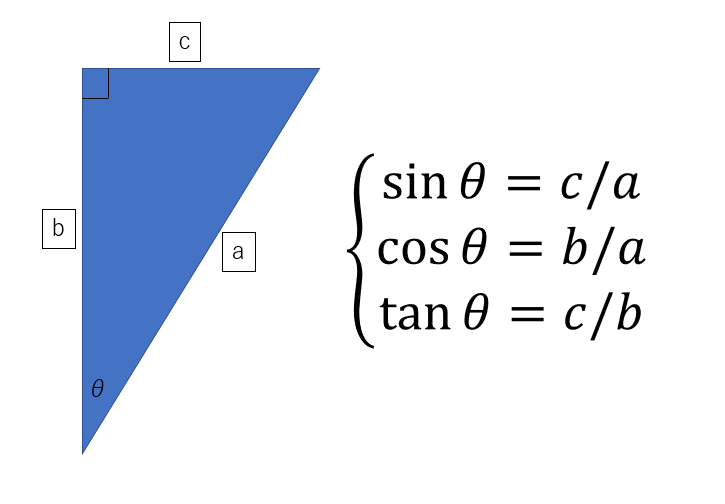
では上記前回のイメージ図もタンジェントで整理し直します。
上図では半径を1として書き込みましたが今回は1/cosθとして書き込んでみます。
右の三角形についてa、b、cを求めます。
| $$ a =\frac{1 }{ cosθ} $$ |
| $$ cosθ = \frac{b }{ a} = \frac{b }{ \left(\frac{1 }{ cosθ}\right)} \\b = 1 $$ |
| $$ sinθ = \frac{c }{ a} = \frac{c }{ \left( \frac{1 }{ cosθ }\right)} \\c = tanθ $$ |
左の三角形についてa、b、cを求めます。
| $$b = 1$$ |
| $$cosφ = \frac{b }{ a} = \frac{1 }{ a} \\a = \frac{1 }{cosφ}$$ |
| $$tanφ = \frac{c }{ b} = \frac{c }{ 1} \\c = tanφ$$ |
求めた数値を書き込んでみます。

画面(弦)の部分をタンジェントで表すことで見やすくなりました。
モニターディスタンスの導入
| $$\frac{\mbox{[変換先アス比]} }{\mbox{ [変換元アス比]}}$$ |
アス比による視野角変換式中のこの部分を書きかえます。
16:9→4:3の変換で係数は3/4=0.75でした。これは水平方向に4:3画面が16:9画面の75%の長さであるということです。
つまりアスペクト比の比は変換前後で画面上の長さの何%であるかということを表していることがわかります。これは画面上の距離ですからモニターディスタンスです。
この画面中央から端まで、変換前後で何パーセントかというのがモニターディスタンスでありMD〇%と表します。
腰だめ時を変換前、ADS時を変換後とすると画面上で何%の位置までズームするかを考えることでADS時の視野角を求められそうです。
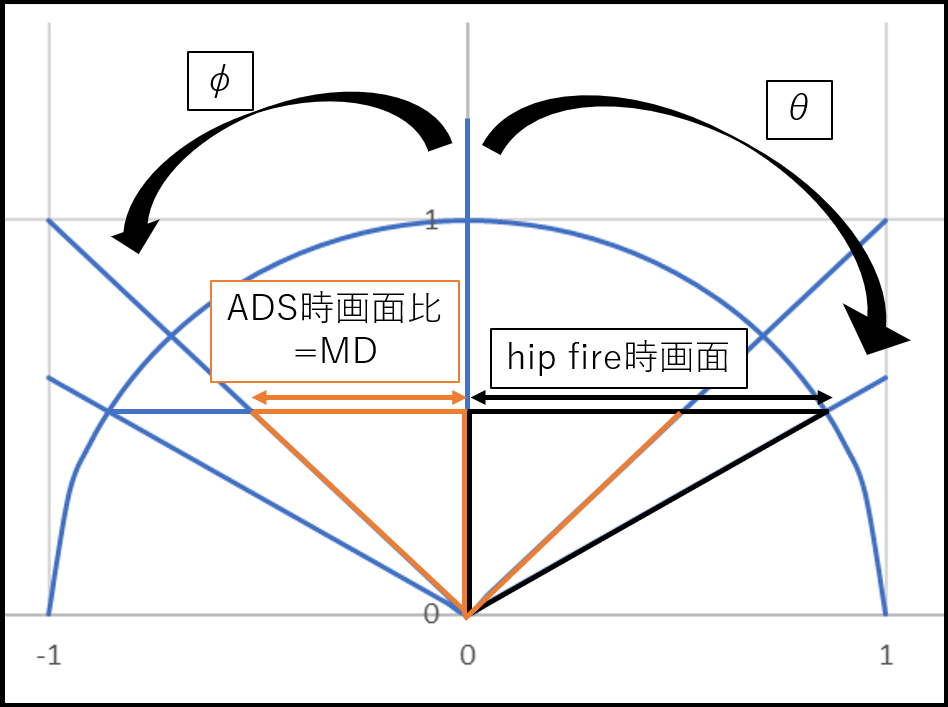
では係数をMDに置き換え前回同様に変換式を求めてみます。
この時の満たすべき条件は、画面の長さ割合をMDとして
| $$ \mbox{ [ADS時画面比]} = \mbox{ MD}* \mbox{ [hipfire時画面]} \\ex) \mbox{ [4:3画面長さ]} = 0.75 * \mbox{ [16:9画面長さ]}$$ |
となればよいです。画面長さ( c )は先程求めましたね。代入します
| $$[ADS時画面比] = \mbox{ MD} * \mbox{ [hipfire時画面]} \\tanφ = \mbox{ MD} * tanθ \\ φ = atan( \mbox{ MD} * tanθ )$$ |
radをdegに直します
| $$ \mbox{ [ADSfov]} \frac{\pi }{ 360} = atan \left[ \mbox{ MD} * tan \left( \mbox{ [hipfire fov]} \frac{ \pi }{360} \right)\right] \\ \mbox{ [ADSfov]} = atan\left[ \mbox{ MD} * tan\left( \mbox{ [hipfire fov]} \frac{ \pi}{ 360} \right) \right]\frac{360}{\pi}$$ |
腰だめ視野角と、ADS時に画面の何%までズームするかわかればADSfovが求められることがわかりました。
ADS視野角を求めてみる
スクショを取ってADS視野角を求めてみます。スクショを取ると横1920ドットですね。画面半分だと960ドットになります。
ズーム時の画面割合がMDなので
| $$MD=\frac{\mbox{960-[ズーム分]}}{960}$$ |
となります。先ほどの式のMDに代入します。
| $$ \mbox{ [ADSfov]} = atan\left[ \frac{ \mbox{960 – [ズーム分]} }{ 960 } tan\left( \mbox{[hipfire fov]} \frac{ \pi}{ 360} \right) \right] \frac{360}{\pi}$$ |
ただこの計算式では画面中央から端までの比ですから、すべて16:9HFOVでしか求められませんので主流である4:3fovにはその都度変換し直さなくてはなりません。
スクショからADS視野角を求めてみました↓
[計算機]スクショからADS視野角を計算する-Screenshot ADS FOV Calculator
まとめ
視野角はタンジェントで考えられることがわかりました。またモニターディスタンスを考えることで画面上の長さと視野角を結びつけることができました。

コメント