視野角はFOVタイプによって数値が変わるためアスペクト比に応じて変換する必要があります。大体CS:GOは1:1fov74、4:3fov90、16:9fov106ということは有名ですが、どうやって相互に変換しているのかという話です。
前の記事:FPSとFOV① 視野角の種類とイメージ
三角関数について
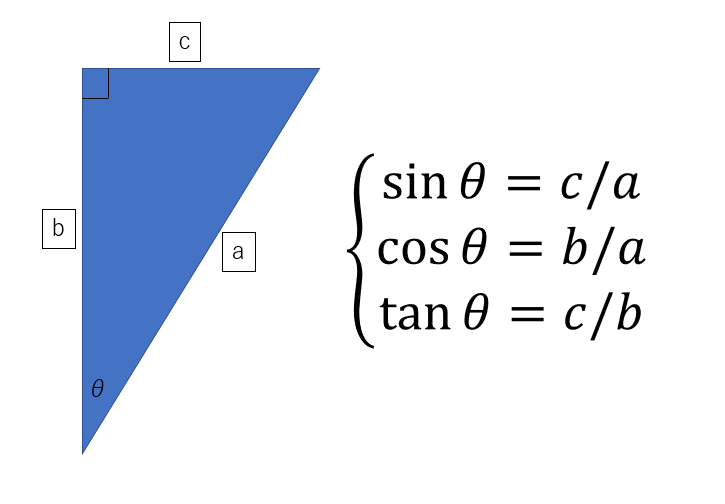
角度θ、辺a、b、cを持つ図のような直角三角形についてサインコサインタンジェントはこの式のように表せます。
16:9FOVから4:3FOVへの変換を考える
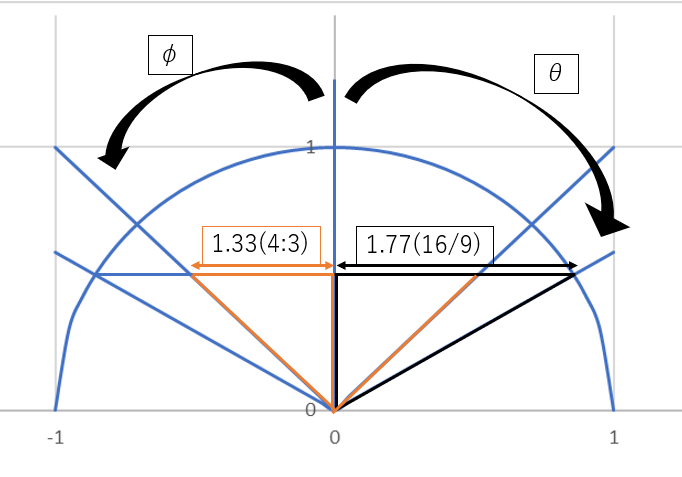
θ の部分が16:9モニターの右半分で見えている範囲で、φの部分が4:3モニターの左半分で見えている範囲です。
画面上で縦の視野角を合わせると4:3fovは16:9fovの75%の横幅を持ちます。
| $$\frac{ 4 }{ 3 } ÷ \frac{ 16 }{ 9 } = \frac{ 12 }{ 9 } ÷ \frac{16 }{ 9 } = \frac{1.33 }{ 1.77} = \frac{3 }{ 4 }= 0.75$$ |
2つの画面長さ(↔の部分)がこの75%の幅を持つという条件を満たせばよいわけです。
また16:9fovを4:3fovに変換し角度を求めるわけですからφをθの関数で表したい。

まず右の黒い三角形16:9fovについて考えます。半径は特に意味もないので1とします。
三角関数からそれぞれの辺の長さが求まりますね。
| $$a=1 \\cosθ = \frac{b }{ a }= b \\sinθ = \frac{c }{ a} = c$$ |
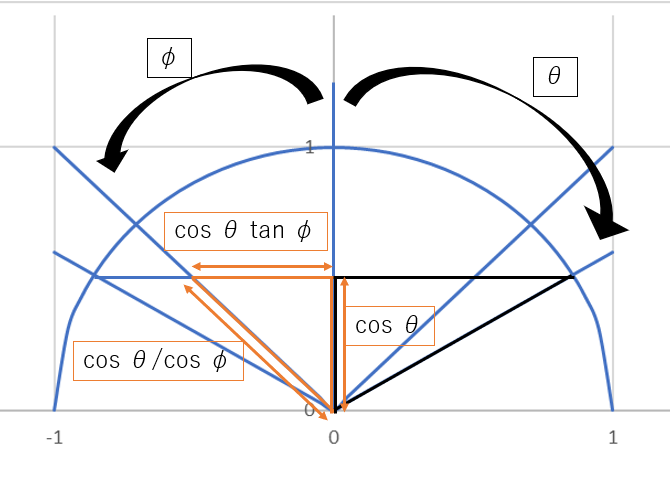
次に左のオレンジの三角形の辺の長さを求めます。
| $$b = cosθ$$ |
| $$cosφ = \frac{b }{ a} = \frac{cosθ }{ a} \\a = \frac{cosθ }{ cosφ}$$ |
| $$tanφ =\frac{ c }{ b }= \frac{c }{ cosθ} \\c = cosθ tanφ$$ |
「4:3fovは16:9fovの75%の横幅を持つ」という条件を二つの三角形の c について満たせばよいですね。
また、求めたいのはφですからφについてまとめます。
| $$1 : 0.75 = sinθ : (cosθ tanφ) \\0.75 sinθ = cosθ tanφ \\tanφ = 0.75 \frac{sinθ }{ cosθ} = 0.75 tanθ \\φ = atan( 0.75 tanθ ) = atan\left( \frac{3 }{ 4}tanθ \right) $$ |
求めることができました。
θとφではわかりづらいです。三角形を作り画面の半分の角度を用いて計算したので2倍すれば視野角になります。また[rad]だとわかりづらいので[deg]に直します。
| $$2θ[rad] = \mbox{16:9fov[rad]} =\mbox{ (16:9fov[deg])} \frac{\pi}{180} \\θ = \mbox{[16:9fov]} \frac{\pi}{360}$$ |
| $$φ = \mbox{[4:3fov]} \frac{\pi}{360}$$ |
θとφに代入し4:3fovについて解きます。
| $$\mbox{[4:3fov]}\frac{\pi}{360} =atan\left[ \frac{3 }{ 4} tan\left(\mbox{[16:9fov]} \frac{\pi}{360}\right) \right] \\\mbox{[4:3fov]} = atan\left[ \frac{3 }{ 4} tan\left(\mbox{[16:9fov]} \frac{\pi}{360}\right) \right]\frac{360}{\pi}$$ |
16:9fovから4:3fov を求める式ができました。
アスペクト比に応じて視野角を変換
ここで式中の3/4に注目します。3/4はどこから出てきた数字でしょうか。
| $$\frac{ 4 }{ 3 } ÷ \frac{ 16 }{ 9 }= \frac{3 }{ 4 }$$ |
この条件式でした。こう書き直すことで一般化できそうです。
| $$\frac{3 }{ 4}= \frac{4 }{ 3} ÷ \frac{16 }{ 9} → \frac{\mbox{[変換先アス比]}}{\mbox{[変換元アス比]}}$$ |
| $$\mbox{[出力fov]} = atan\left[ \frac{\mbox{[変換先アス比]} }{\mbox{ [変換元アス比]}} tan\left(\mbox{[入力fov]} \frac{\pi}{360}\right) \right]\frac{360}{\pi}$$ |
一般化できました。サインコサインタンジェントを図に書き込んでいくだけなので簡単です。

コメント