- Home
- 一覧
-
Logicool G PRO HERO マウスレビュー
Logicool Gの左右対称小型マウスPRO HEROをレビューします。
通称卵、所謂GPRO有線、G102 、G203、G304と同形状のマウスです。
手元のものは型番はG-PPD-001tで新しいモデルとなっています。
G-PPD-001は3366センサーで編組ケーブル、スイッチがOMRON D2FC-F-7N(20M)
G-PPD-001rはheroセンサーになり柔らかいゴムケーブル、スイッチがD2FC-F-K(50M)
G-PPD-001tはスイッチがD2FC-F-7N(G1)と変更されています。
ちなみに002がWLで003がX SL
スペック
メーカー ロジクールG ツイッター @LogicoolG 製品ページ PROゲーミング マウス 形状 左右対称 長さ 116.4 mm 幅 62.2 mm 高さ 37.4 mm(ソール抜き) 重さ 85 g スイッチ D2FC-F-7N(G1) センサー HERO25K 最大速度 400以上 IPS / 85 G LOD 1 mmちょい DPI 150-25.6K(50刻み) ポーリング 125/250/500/1000 Hz ソフトウェア ロジクールG HUB 形状
全長116.4 mmと短い卵型の形状の左右対称マウスです。
上下


サイズ感
ボトム中央の幅が50.4 mmと狭く全長も短い小型マウス。
リア
卵型の形状で尻に幅がない。
ボトム
ボトムは50.4 mmの幅が一定。
トップ
ボトムの幅は変わらず一定ですがトップは中央が最も太くフロントとリアに細くなっていく。
逆台形度
ボトムとトップの形状からわかる通り中央の方が逆台形が強くフロントに向かって弱くなっていますがフロントの逆台形度も6.7 mmと大きい。
センサー位置
センサー位置重心ともに中央。
横

トップ
TOPは中央から15 mm程度後方にあります。
37.4 mmの高さがありなだらかな尻で緩く落ちていく。
MB
ガイドがある平らな感じのMB。
前後


平らなトップ
サイドはやや外側に弧を描いている。
特徴
- L 116.4 x W 50.4-62.2 x H 37.4 mm
- 卵型の形状
- ボトムはフラットで強い逆台形
- なだらかなトップ
- 中央なセンサー位置
比較
中身
分解





ピンアサイン 3 mmと厚みのあるシェル。尻のシェルは単体で13 gあるのでつまみ持ちの人は外すだけで結構軽くなる。
ホイール
kailh製のエンコーダで静かに回りノッチ感がしっかりある。
クリック
スイッチがOMRONのD2FC-F-7N(G1)。古い型番はD2FC-F-Kだったはず。こっちの方がいい感じ。
PRO WLがチャタリング多発しすぎてスイッチが変わった記憶があるが関係なかったっけ。私のはチャタってないのでわからない。
軽く歯切れよくストロークも丁度良く非の打ち所がない。

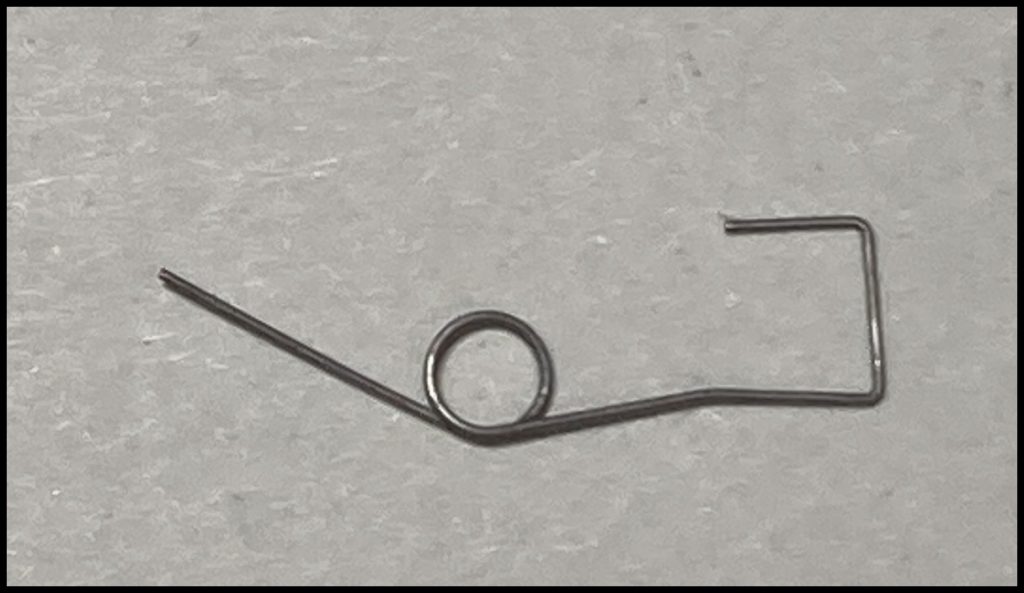
バネが入っており押し下げをアシストしてくれて柔らかく、初動が軽くなり動作点までわずかにストロークが短くなる。
このばねを外すとより歯切れよくなり連打しやすくなると感じた。有り無し試してみるといいと思う。
サイドボタン
サイドボタンがある。
ケーブル
柔らかいので取り回しはいいがパラコードケーブルがあるなら交換した方がいい。
センサー
いい性能。
LODは1~1.5 mmぐらいと短くちょうどいい。
ソフトウェア
Ghubで設定
- DPI:150-25.6K(50刻み、最大5ステージ)
- 125/250/500/1000 Hz
- 6ボタンに自由度のあるボタン割り当てが可能
- テールとロゴ部分にライティング設定可能
- オンボードメモリ(プロファイル5つ)
グリップ
サイドは逆台形が強くやや中心が太いが幅にあまり差はない形状。
ボトムの幅だけでいえば多くの小型マウスよりも細く挟み込みやすい。
くびれがなく指に引っかかりがないので安定感は得にくいが持ち上げやすい。のでグリップテープ等を貼るのもあり。
まっすぐ持つと左右で挟み込むような感じで、センサーを傾けさせて持つと手前に引き付けるように持てる。
重さ
85 gとやや重い。重心は中心で持ち上げやすい。
コーティング
トップはマット、サイドは軽い梨地加工。
つまみ
小型マウスでつまみやすいが重い。
つかみ
持ちやすい。フィット感は得にくいがしっかり動かせる。
おわり
重さはあるがクリック感がよく性能も申し分ない。
5000円帯のマウスでは特に性能ビルドクオリティよく形状合えば買わない手はない。
ぜひ軽量版を公式に出してほしいところだがそんなことはなさそう。
前の記事:[雑記]Logicool G502 3366 感想とか
次の記事:ZYGEN NP-01 マウスレビュー
感想
S2と似ても似つかないのにフィーリング似てるなと思ってたんですがたぶんどちらもフロントの逆台形強いとこが似てて薬指の感じが親近感沸いてたんだろう。
軽量版でないかなあ。
-
[雑記]Logicool G502 3366 感想とか
Logicoolの多ボタン左右非対称ゲーミングマウス G502 3366 を紹介します。
これぞゲーミングマウスというかっこよさがあり無線で性能もいいという、1つのコンセプトとして完成されているように見える G502WL 。
気になりますが気軽に試せる値段でもなくとりあえず試すために中古で G502 3366 を購入しました。
スペック
メーカー LogicoolG ツイッター @LogicoolG 製品 G502 3366 形状 左右非対称 重さ 125 g~(おもり要素) スイッチ OMRON D2FC-F-7N(20M) 割り当て可能数 13 センサー 3366 LOD 1.1 mm, 較正1 mm未満(ソール0.55 mm) DPI 50-12k(50刻み) ポーリング 125/250/500/1000 Hz ソフトウェア ロジクールG HUB 形状
左右非対称のマウスですがIE系とはやや異なるタイプの形状です。
全長130 mmと長そうだがMBの先がとがっている分な気がする。
高さ41 mmぐらい
親指あたりの幅58とか。対称マウスと比べるとやや太いがフロントに行くにつれて細くなっている。


尻は左サイドより右サイドの方が膨らんでいて非対称マウスにありがちな母指球が膨らみにあたって痛いということは起きにくい気がする。まっすぐ持った時の話で斜めにセンサー傾けて持つとまた変わってきそう。
右サイドはフロントに向かって細くなっていく ハ の字。


トップの形状は緩ーく右下がりで軽いチルトグリップを想定していそう。


右サイドは中央あたりは台形だがフロントは逆台形となっている。


右MBは膨らんだ形状で右サイドに向かって曲線を描いて低くなっていく。右サイドとつながるかのようで、中指薬指小指を流れに合わせて持つといいのかもしれない。右MBはトップというより右サイドのパーツというような感じか。
左MBは深めのガイドがある。
分解・組み立て
G502めちゃくちゃパーツ多くて1回目に分解するときは手間取りました。のでその苦労をお届けします。
組み立てなので分解は下から


ホイールをクリアパーツに戻し、黒いカバーのようなパーツをはめ込み裏をねじ止め

ケーブルとブッシュを固定はめ込み、ブッシュ上部にクリアパーツを載せます。
センサー基板を載せスペーサを挟みねじ止めします。

基板を載せ3か所ねじ止め。黄色の丸いホイールクリック脇の穴に小さいネジを入れます。最初分解するときにばねを吹っ飛ばして探すのに苦労してしまいました。
ホイールパーツを固定する黒い部品を基板上に固定します。

ホイールパーツを載せ穴に棒を差し込むことでホイールパーツを固定します。

マグネットをはめ込み、サイドボタン基板を溝にはめます。


サイドボタンを組みネジ止めします。シェルにはめ込みねじ止めします。

シルバーのパーツをはめねじ止め。


クリック横のボタンをはめねじ止めします。

その前のボタンもはめてねじ止め

先に左クリックを固定します。


RGB用のパーツをはめねじ止め、シェルをはめます。


尻部分のシェルを3箇所ねじ止めし、残りのボタンパーツを固定します。
上下合わせてねじ止めし組み立て終わりです。
最初分解したときは結構手間取りました。設計の人は良く考えたもんだと思う。
なくても使えるものではあるがホイール下のばねは初見殺しなので飛ばさないように気を付けたほうがいい。
比較
vs gpwl
サイズは同じぐらい



vs ec1
IE系とは全然違う感じ




中身


ピンアサイン これだけパーツがあれば重いはず。すごい数。
G502 WLでは構造がG PRO WLのように内側にフレームがあるタイプに一新されているのが公式サイトからわかります。この構造で軽量化を図っているらしい。
いろいろ軽量化したとしても元が125 gではいくら頑張っても80 g台にはならないと思うのでだったら重さを楽しんだ方がいいかもしれん。
クリック


メインは20Mのもの、サブボタンは耐久値の低いモデルを使用しています。サブボタンのクリック感もメインに近くていい。
先端部分を押すとロジらしいクリック感があります。スイッチが結構前方に配置されていることからか根元やホイール横あたりを押すとOMRON 20Mにしてはちょっと重め。
ホイール
ホイールはVaxeeやZowie無印モデルのように回すと大きな高い音が鳴ります。光学ホイールです。
ホイールクリックは重いですが左右チルトボタンは軽いです。
ホイールの軸でクリックするホイールクリックでなくホイールを直下に押し込むタイプ。
最近では左右チルトあるわけではないですがRoccatやVaxeeやZowieも直下に押し込む構造ですね。
チルトはこの構造がいいのですかね。チルト無いなら製造コストがかかるだけな気もします。あまり使用感で差がない気がする。
スクロールは大きな音でノッチ感のある回転とフリースピンの2種類で両極端な気もします。
ケーブル
ケーブルは硬いですが本体に重量があるのでどんなケーブルでも何も気になりませんね。
センサー
3366センサーでほぼ文句なし。LODも1 mm未満に設定できて短い。キャリブレーションできる。
ソフトウェア
Ghubで設定を行えます。
DPI、ポーリングレート、ボタン設定、キャリブレーション、ライティングの設定。
ボタン割り当てが13か所にできます。

私はLEDを消しました。ボタン多すぎて逆になに割り振るか困りますが使いこなせたら効率がすごくなりそう。
グリップ
125 gと重いです。現在ラバーをはがしグリップテープ、底面パネルとマグネットを外し110 gです。
重心は中央でセンサーよりちょっと前です。
側面がラバーコーティングというかゴムが貼ってあります。使い始めは良さそうですが汚れや持ち方によってはえぐれていくので私はあまり好きではないですが滑らず弾力もあるでグリップ力はあります。
凹凸のないGPROWLを非対称エルゴノミクスにしたような大きさと形状です。いわゆるIE系の手全体と密着させるような形状ではないです。右側面は軽い台形から軽い逆台形になっています。
右クリックは指のガイドがなく盛り上がっているタイプ、左クリックは指のガイドがありくぼんでいるタイプと左右で異なっています。
左右で指の置き心地が異なりますが、高低差を考慮しての設計だったりするのでしょうか。それとも単純にサブボタンの設計上とかだったりするのでしょうか。
かぶせ
サイズ的にも非対称な形状からもかぶせ持ちにあっています。フロント部は軽い逆台形になっているので左右非対称の中で持ち上げやすい部類です。GPROWLをエルゴライクに持っている人にははまりそう。
つかみ
右側面が非対称マウスとしてはフラットな部類で非対称としては幅が細め。
クリック部は左が高く右が低い形状ですが尻の部分は軽微な右下がりで非対称ですがチルトグリップでなくとも手のひらに違和感はなく持ちやすい部類です。
小指がまげて中央あたりに配置すると側面がやや台形で、伸ばして奥めに配置すると逆台形なのでグリップ感が異なる。
つまみ
ホイール位置がちょっと後ろめだからかもしれませんが最初にぱっと持ってみてくださいと言われたらつまみ持ちで持つ気がします。
MBが高めなこともありわしづかみというよりは指を伸ばし気味なつまみ持ちがしやすいです。
おわり
他にはない特徴的な形状で面白いですね。RazerのBasiliskが似たような形状らしいです。
多ボタンでフリースピンもついておりギミックが凝っていますがホイールは重いか軽いかの両極端でバランスが悪い気もします。重いですが性能高くFPSで使えますし、多ボタンなので作業用にもいい。
重めのマウスを使いたいときに90 gのマウスとかでもいいですが100 g越えと振り切っているg502の方が使っていて楽しいし重さを活かしたエイムができる気がします。重さが欲しいときはg502一択でいいんじゃないかと思った。性能いいし形状も特徴はありますが持ちやすいし。
試しにG502を買ってみて無線版を買うか?という話題でしたが欲しい!
前の記事:Zowie S1-C マウスレビュー
-
[自キ]手配線でホットスワップ対応のキーボードを作る
手配線でホットスワップキーボードができないかと思い試しに作ってみました。自キ制作レポートです。
設計方針
前回の分割キーボード制作で手配線のやり方は自分の中で結構納得がいったので手配線でホットスワップ対応のキーボードが作れないかと思い試作してみることにしました。
手配線でホットスワップというとミルマックスが思い浮かびそうですがkailhソケットで作りました。こちらの方が安いし簡単だと思ったので。
出来上がり

4キーなのもあってぱっとできました。
考え足りずソケットむき出しで抜くときに引っ張られてしまったためボンドで固定しました。
キーキャップを引き抜くとスイッチごと抜けてしまうのでトッププレートはきつく設計する必要があるかもしれません。キーキャップ交換しないのならこれでもいい気がします。
アクリル積層は打鍵感は硬いですが打鍵音は結構いい感じなんですね。

次作るときは4層にして部品を押さえればよさそう。
材料
アクリルカット
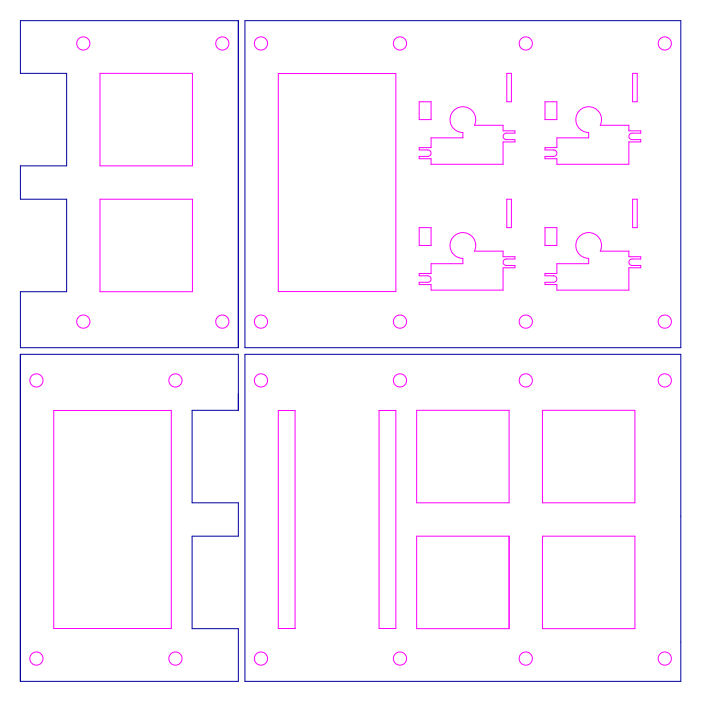
参考:スイッチ用PCBソケット(10個入り) – 遊舎工房 (yushakobo.jp)データシート
参考:Kailh BOX スイッチ(10個) – 遊舎工房 (yushakobo.jp)データシート
Acrylic Laser Cutting – Order Online (elecrow.com)にて2.5 mmのアクリルカットを注文した。
試しだったので最小サイズの10×10で収まるように。
3層アクリルプレート。上2枚はキースイッチ用の四角い穴でボトムプレートとの間にはナットを挟む。
ボトムプレートはキースイッチの足、kailhソケット、ダイオード固定用の穴をあけた。
思い立ったが吉日さっと書いたのでソケット固定できていなかったりと残念な点が多い。立体を頭の中でうまく組み立てられていない気がする。
組み立て
アクリルプレート

アクリルプレートが届きました。かわいい?キーホルダー付きです。

こんな感じで3層になります。
kailhソケット


こんな風になってるんですね。シンプルだけど実用的で偉大そう。

ボトムプレートにソケットを乗っけます。きれいにはまってくれてよかったです。
はんだ付け部分を2か所引っかけているだけなのでぐらつきます。
配線

ダイオードとワイヤーを配線しました。アクリルに乗っけてはんだ付けするだけなので簡単です。
組み立て

トッププレートを。ネジ止め。2枚重ねてナットで締めます。

ボトムプレートもネジに差し込みねじ止め。
promicroを上からはめ下からはんだ付け。

上から見てソケット丸出しなことにこのときやっと気づきました。図面書いてた時にはソケット上に1枚あると思い込んでいたんです。
キースイッチ

スイッチを挿してみました。ソケットにぶっ刺さってる。
このままだと抜くときにソケットが上に引っ張られるのでボンドでソケットを固定しました。
完成

ボンドが汚いですが無事完成。
余分なねじを切り落としてゴム足付ければそれっぽくマクロパッドとして。
反省点
手配線でホットスワップのキーボードを自作することができることを確認した。
利点はpcbを設計しなくていいこと、配線が透けて見えてなんかいい感じなことです。
欠点はpcb設計すればそれで済むじゃん。
アクリル4層にすれば今回問題となったソケットの固定はクリアすることがでる。その場合上は5 mmを1枚もしくは2.5 mmを2枚だろうか。下2枚はできるだけ薄い方がよく2 mmを2枚になりそう。厚みは1cm+ゴム足ぐらい。
できれば1.6 mmとかがいいですが、となるとFR4なのでpcbを設計しろの一言に尽きる。手配線でキーボード作るのは完全に工作趣味でしかない気がします。pcbの方が安上がりだし。
また今回promicroをめんどくさいやり方でつけましたがpromicroは裏側に張り付けて配線できそうです。今回の場合そうすれば厚みはその分増しますが10×10サイズで6キーのマクロパッドができそう。
あとは配線用にもっと細い単線のワイヤとか用意しておけばやりやすそう。
10×10のサイズで気軽にいろいろ試してみるのは面白いかもしれない。でも試すだけならブレッドボード使った方がいいじゃん。
いい加減pcb設計しろ
前の記事:[雑記]PulsarGamingGears メカニカルスイッチテスター
次の記事:[雑記]TALPKEYBOARD Gateron CAP キースイッチセット 比較
-
Zowie S1-C & S2-C マウスレビュー
Zowieの左右対称マウスS1-C及びS2-Cをレビューします。
Sシリーズを軽量化した新しいモデルで旧Sシリーズと比較します。
また、ZOWIE Cシリーズはケーブルブッシュを折れ曲がったタイプからストレートで大きなものにマイナーチェンジしましたが、その新旧ロット間での差異についても見ていきます
形状等変更点のない部分はこちら:ZOWIE S1&S2を比較 マウスレビュー
スペック
メーカー BenQ ZOWIE 製品ページ S1-C ゲーミングマウス for e-Sports ZOWIE S2-C Symmetrical eSports Gaming Mouse 重さ 74.3 g 71.4 見た目



外見はケーブルブッシュ以外同じ。

新ロットではブッシュが太く長くなっています。ケーブルを引っ張ってみると大きくしなり、保護要素としては良さそうですがだいぶ見た目があれですね
ロット間でブッシュだけでなくホイール周りも変更が入っていますが口述します。

付属品

交換用のソール1セットが付属。ZOWIEの純正ソールは0.45 mmと薄い。
zowie純正ソールは滑りの質がいいと感じます
中身
分解




ピンアサイン - 全体的に薄くなり中間シェルは肉抜きされ89 g → 74.3 gに軽量化
- 基板周りの構造変更
- マイクロスイッチの位置がフロントに寄った。
- チルトクリックから直下クリックにホイール構造の変更
- 疑似パラコードに変更しやや太くなったが3割ほど軽量化
ホイール
16ステップから24ステップの光学ホイールに変更。回転数に対するスクロール量は多くなった。
S1よりS1-Cの方が重く硬くうるさくなった。Vaxeeよりも重く硬い。
ノッチ数を増やしても重く硬かったら意味がない気がする。相変わらずスクロールはしにくい。後述するが分解してばねを弱めれば軽くすることはできる。
ホイールクリック押下部にゴムが巻いてあるが誤クリック防止だろうか。外した方がホイールクリックは軽くなる。が誤爆するようなら戻した方がいいかも。
ZOWIE Cロット間でのホイール部品の差異
右の白いものが旧ロット、左が新ロットです。
まず色が異なるのが目につきます。素材など分かりませんが、比較したときに左灰色の新ロットのホイールジグの方がホイールの回りが悪いです。白い方がスムーズに回転します。
そしてノッチ感を出すための部品がこの黒いパーツですが、旧ロットでは板バネがあるのにたいし、新ロットでは見えませんが、通常のばねを差し込む構造に戻っています。


なので最後に紹介しているハンフリースピン化するカスタムは旧ロットでしか使うことができなさそうです。
クリック
マイクロスイッチがフロントに寄ったことでストロークが短くなり返りがよく、歯切れよくなった。そのためクリック感がやや硬く重くなった。
S1独特のクリック感は失われたがS1-Cの方が万人受けしそうなクリック感をしていると思う。
サイドボタン
分解組み立て時にシェルに引っ掛けてサイドスイッチが壊れた。
ので分解するときはシェルをサイドスイッチに当たらないように気を付けましょう。
ケーブル
やや芯がありやや太さがありやや重い。S1のケーブルより軽く柔らかくなっている。
悪くないが最近のマウスはこれより柔らかく軽いものも多いと思う。
設定
ユーザーガイド


- DPI:400(赤)/800(紫)/1600(青)/3200(緑)
- ポーリングレート:125/500/1000 Hz
- LOD:低・中・高に設定可能
- デバウンス:高速・標準に設定可能
Zowieはデバウンスが長いといわれていたがCシリーズで改善したらしい。LODは変わらず短めで、高に設定しても変わらなかった。やり方が悪いだけかもしれない。
おわり
Zowie S1-Cは15 g程度S1から軽量化されているがそれでも74.3 gと普通な重さ。
クリック感はS1より少し硬めになり歯切れよくなっている。
ホイールは24ステップになったがより重くなった。
パラコードケーブルになった。
新しく買う人はいいが軽量マウスにはなっていないので買い替えるほどではない気がする。
次の記事:[雑記]Logicool G502 3366 感想とか
感想
よくなった点はやや軽くなったこと。気になった点は全体的に。
ケーブルはやや太く硬い。ホイールの回りがS1より回しにくい。
これは完全な好みだけどS1独特の宙に浮いているかのような軽いクリック感はとても好みで、歯切れよくなったとはいえ軽いS1の方が私は好き。
分解し組み立て直したときクリックがシェルをかぶせた時点で押されてしまい何度組み直しても治らずめんどくさかった。箱出しではどう収まっていたのだろうか。内部にフレームを入れるというのもGPWLぐらいがっちり固定しているのなら安定するのかもしれないが結構ふにゃふにゃだしあまりクオリティがよろしくない気がする。何ならネジ穴が一か所最初からなめていた。
クリック部分のPCBがトップマウントから変更されフレームにマウントする形となった。トップマウントであれば起こりえなかったはず。G PRO WLからVAXEEの流れで内部フレームトップマウントの形式が主流になるのかなと思っていたのだが。
私は持っていないがZA13-Cでサイド押すとサイドボタンが押されるみたいな話もいくつか見かけたし現時点でのCシリーズの設計はあまりよろしくないのかもしれない。が。微妙な個体引いただけかもしれない。
あまりいいと思える部分が少なかったので個人的にはS1からわざわざ買い替える必要はないと思った。しかし軽量S2クローンは多くあっても軽量S1クローンは見かけないので選択肢はこれしかない。
軽量化(軽量マウスではない)とトレードでビルドクオリティが落ちたなと思う。
だが63 gに軽量化されたS1の使い勝手は単純に快適すぎるので最終的に満足している。でもS1のクリック感の方がいいなあ。
、、、、、、S1も頑張ったら軽量化できるのかな、、、、、、?
カスタム
ホイール


ホイールの中に玉が入っておりこれがスリットに当たってノッチ感を出していて取り外せばG502のフリースピン状態になる
玉を乗せている板の角度を変えてやればホイールの軽さを調整できる
軽くすれば緩くなるので少しおもちゃっぽくなったが重いのは使いづらいので満足


余談だが左が旧zowieのホイールで機械式のエンコーダと同様にホイールに軸をぶっさす構造ノッチ感は玉をばねでホイール内周に押し付けることで出している。
右がVaxeeのホイールでzowie-cと同じかと思いきや異なる。軸をぶっ刺さず直下クリックするのはzowie-cと同じだがノッチ感を出す構造は旧zowieと同じでばねで押し付ける構造。またzowie-cの方がやや径が大きい

旧zowieとvaxeeは中身は同じでzowie-cとvaxeeは外見が同じ感じ。
zowie-cの唯一のいい点はば板バネを緩めて半フリースピン状態にできることでブラウジングがはかどる。
軽量化
軽いS1が使いたくてS1-Cを購入したので軽量化した
底面、中間シェルの肉抜き
サイドボタンの除去。というかサイドスイッチ吹っ飛んで壊れた。一応スイッチ交換すれば直るが。
中身の骨組み後ろ側除去
4つ編みケーブルに交換
サイドにグリップテープ
63 gに軽量化できた
個人的には十分軽くS1を使いやすくなった
S1唯一の欠点は重いことだったので満足。旧S1だとおそらく肉抜きしても70 gを切れるか切れないかだと思う。


-
Logicool G302 マウスレビュー
新しく発売されたG303SHはG303を大きくしたような形状ということです。元となったG303形状を触ってみたいなと思いました。
G303は売っておらず形状が同じG302をAliexpressにて購入したのでレビューします。
他にはない菱形形状が特徴のマウスです。G302の紹介ですがG303も形状は同一です。
スペック
メーカー LogicoolG ツイッター @LogicoolG 製品ページ G302 形状 左右対称 長さ 114.8 mm 幅 65.4 mm 高さ 38.4 mm(ソール0.7 mm抜き) 重さ 90 g スイッチ OMRON D2FC-F-7N(G1) センサー AM010 最大速度 120 IPS / 20 G LOD 2 mm DPI 300-4k(50刻み) ポーリング 125/250/500/1000 Hz ソフトウェア ロジクールG HUB 形状
G302は全長114.8 mmな小型の左右対象マウスでひょうたん型でなく菱形で中央が最も膨らんでいる形状です。
上下


サイズ感
全長が短い小型マウスですが高さが割とありつまみ持ちするよりつかみ持ちする方がやや大きく感じます。
リア
通常尻がある部分がひし形となっていて抜け落ちています。
中央
前方から75 mm程度、後方から40 mm程度の後方部分が最も幅が広く65.4 mmあります。
フロント
底面を見ると太い部分が54.8 mm、前方は42.7 mmとなっておりフロントへ細くなっていきます。
逆台形度
中央あたりが10 mm、前方が10.8 mmとフロントに行くほど逆台形が強くなっていきますがほぼ一定です。
逆台形度がかなり大きな形状になっています。
センサー位置
センサー位置は中央です。
横


トップ
TOPは中央から15 mm程度後方にあります。38.4 mmと小型マウスとしてみると高め。
MB
クリック部分が全体的にやや凹んでおりガイドがあるやや高めのMB。
前後


非常に平べったいトップ。逆台形が強いサイド。
特徴
- L 114.8 x W 65.4 x H 38.4 mm
- 中央のセンサーと重心
- ひし形の形状と強い逆台形
- リア寄りで全長のわりに高いトップ
比較
中身
分解




ピンアサイン G302ネジが多い。基板の下にある透明なプラスチック片は絶縁のためにあるとか聞いたことがあります。ねじ自体を取り外してしまえばなくても大丈夫です。
90 gと重いので肉抜きした方が使いやすいかもしれない。私は80 gまでボトムとサイドで肉抜きした。
ホイール

光学式ホイールで回転が重めで音も大きめですがG502とかZowieとかVaxeeほどではなく、しかし少し擦れるような感じがする。
ホイール保持部分がシェルの一部になっていて面白い構造。MBのようにシェルがたわんでホイールクリックを行います。
クリック
スイッチがGPROWLとかGPROHEROのスイッチが変更されたロットに搭載されているD2FC-F-7N(G1)。
普通の20Mだと思っていたというかAliのストアの写真でも普通の20Mだったが。中国だと結構このマウスは生産されているのでしょうか。ロットによって変わりそう。
また押下部にバネが仕込まれていて少し下に力が加わっています。プレス開始時に補助してくれますがリリースが独特な感じになります。
Logicoolらしいクリック感です。Gproheroを少し硬めにした感じで柔らかくぱちぱちしていて歯切れよい。
サイドボタン
やや上を向いているので少し押しにくく感じることもあるかもしれない。とくになし。
ケーブル
細く重く芯がある。交換した方が使いやすいかも。
センサー
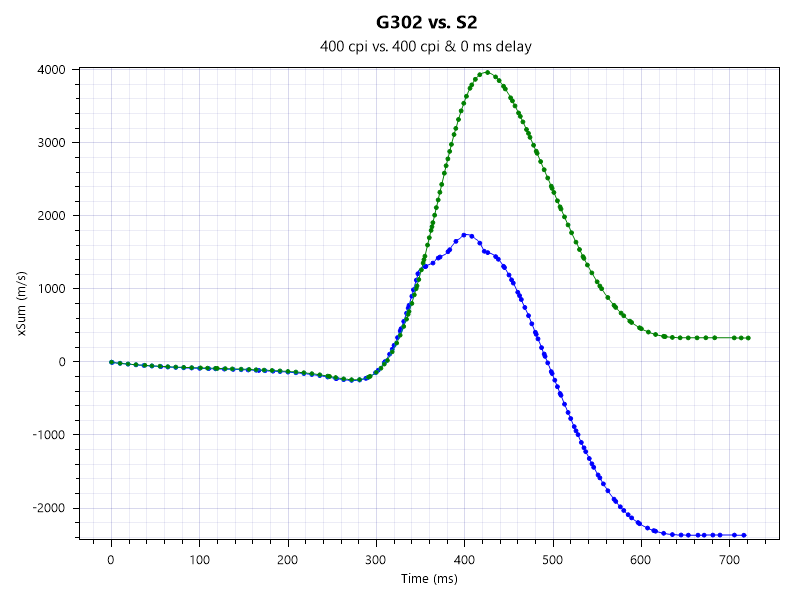
私が早く振って160IPS程度ですが性能が120IPS/20Gなので性能が足りずフリックするとずれ120IPS超えるとカウントが飛び読み取らなくなる。FPSで満足に使うことはできない。
センサー遅延はZowieマウスと比較して見られません。
LODは2 mmと長い。
ソフトウェア
G HUBで設定
- DPI:300-4000(50刻み、最大5ステージ)
- 125/250/500/1000 Hz
- 6ボタンに自由度のあるボタン割り当てが可能
- サイドとロゴ部分にそれぞれライティング設定可能
- オンボードメモリ(プロファイル1つ)
OnboardMemoryManagerでも設定可能だがDPIが中途半端な値でしか設定できない。
グリップ
重さ
90 gと肉抜きしないと重い。重心は中央で持ちやすい。
コーティング
トップがマットでサイドがちょっと梨地ぽい感じ。GPROHEROと大体同じ
MB
クリック部分のガイドが独特で何とも言えないフィット感がある。
つまみ
全長が短いのでつまみ持ちしやすい。
深くくびれたりしていないのでサイドは持ちやすいが幅があるためわしづかみするように持つことになる。
つかみ
G302はGPROHEROから幅が一回り大きく、よりわしづかみする感じ。
わしづかみにして ハ の字なサイドにひっかけ手のひら側に引き寄せるような感じ。
おわり
G302は安価だがクリック感がよく印象もいい。使い続けているとなんかくせになる。鷲掴みするのに合っていて合わない人は合わない。
センサーがFPS用グレードでないが入手性は高い。G303、G303SHが気になった。
前の記事:HyperX Pulsefire Haste マウスレビュー
次の記事:Zowie S1-C マウスレビュー















![[自作マウス]op18kv2 mod①FDMで様子見てみる](https://tsuiha.com/wp-content/uploads/2026/01/image-15-2.jpg)
![[自作マウス]op1 8k v2 基板採寸](https://tsuiha.com/wp-content/uploads/2025/12/image-12.png)

![[自キ]BNY6X V2 ②GH60互換60%キーボード試作品届いた](https://tsuiha.com/wp-content/uploads/2025/11/IMG_3788.jpg)
![[自キ]チルトテントアルミケースな左手デバイス作る④Nitingale B2](https://tsuiha.com/wp-content/uploads/2025/11/IMG_3549.jpg)
![[BF6]視野角と感度の設定について](https://tsuiha.com/wp-content/uploads/2025/10/image-36-3.jpg)
![[自キ]BNY6X V2 ①GH60互換60%キーボード設計する](https://tsuiha.com/wp-content/uploads/2025/10/image-6.png)
![[自キ]KS-33B Gateron LowProfile 3.0スイッチに希望はあるのか](https://tsuiha.com/wp-content/uploads/2025/09/IMG_3528.jpg)
![[自キ]チルトテントアルミケースな左手デバイス作る③修正](https://tsuiha.com/wp-content/uploads/2025/09/image-2.png)
![[自キ]チルトテントアルミケースな左手デバイス作る②ケース](https://tsuiha.com/wp-content/uploads/2025/08/image-26.jpg)
![[自キ]チルトテントアルミケースな左手デバイス作る①基板](https://tsuiha.com/wp-content/uploads/2025/08/image-24.jpg)


![[自キ]遊舎工房のレーザー加工サービス利用してみた](https://tsuiha.com/wp-content/uploads/2025/08/image-5-1.jpg)


![[自キ]磁気キーボードを作りたい。6週目](https://tsuiha.com/wp-content/uploads/2025/07/image-2.jpg)

![[自キ]磁気キーボードを作りたい。5週目](https://tsuiha.com/wp-content/uploads/2025/06/image-27.jpg)

![[自キ]磁気キーボードを作りたい。3週目](https://tsuiha.com/wp-content/uploads/2025/05/image-15-1.jpg)
![[自キ]磁気キーボードを作りたい。2週目](https://tsuiha.com/wp-content/uploads/2025/05/image-9.jpg)
![[自キ]磁気キーボードを作りたい。1週目](https://tsuiha.com/wp-content/uploads/2025/04/image-25-1.jpg)
![[自キ]50%オーソリニアのキーボード作った OSPREY59O](https://tsuiha.com/wp-content/uploads/2025/03/IMG_2343.jpg)






![[自作マウス]haste2基板を3Dモデルに起こした](https://tsuiha.com/wp-content/uploads/2025/01/image-10.jpg)

![[デスク]VESA拡張してモニターを増設した](https://tsuiha.com/wp-content/uploads/2025/01/IMG_2567.jpg)
![[デスク]充電ケーブルを天板裏に移動してすっきりした](https://tsuiha.com/wp-content/uploads/2025/01/IMG_2565.jpg)

![[自作マウス]マウスシェルモデリング その2](https://tsuiha.com/wp-content/uploads/2024/11/IMG_2288.jpg)

![[イヤホン]moondrop 水月雨 KadenzとKatoの雑話](https://tsuiha.com/wp-content/uploads/2024/11/IMG_2385.jpg)

![[オーディオ]ジェネリックER-4B化モジュールを作る②](https://tsuiha.com/wp-content/uploads/2024/08/er4switch1.jpg)

