- Home
- 一覧
-
[計算機]APEXの振り向きを揃えるADS感度-Apex Sensitivity Converter By 360°
APEXのADS時の振り向きを腰だめと同じにすることができます。
基本的には一番上のスライダーを動かすだけです。設定ファイルから細かく設定している人はclscaleを入力してください。
関連:VLORANTの感度・ADS感度計算機はこちら
[計算機]VALORANTの感度と視野角の仕様を調べてみた (tsuiha.com)
APEXのADS感度を360°変換・振り向き変換
おわり
例えば等倍のADS感度を1.3にして揃えたとして、他の倍率のADS感度はどうするべきでしょうか。まあ試して強かった数値にするのが最強ですが置いといて。
このとき・他のスコープ感度も1.3にすると、等倍スコープ感度を基準としたMD0%変換となります。
他のスコープ感度を1.0のままにすると、腰だめ感度を基準としたMD0%変換となります。
つまり等倍ADS感度倍率と揃えれば等倍が基準となり、1.0のままにすればhipfire基準の感度となります。
なので等倍は1.3だけど他は低めで0.8という人がいたとすると、ほかのスコープは0.8!ではなく
1.3 x 0.8 =1.04も試してみるべきということになります。
関連:[計算機]APEXのADS実質感度と振り向きを計算-APEX ADS Sensitivity Calculato
関連:[計算機]APEXの感度・ADS感度をモニターディスタンスで変換-Apex Sensitivity Converter By Monitordistance
-
Zygen NP-01 マウスレビュー
VAXEEのブランドZYGENから発売されている左右非対称マウスNP-01をレビューします。
NP01はS2をベースとして非対称マウスにした形状ですがS2とは使用感が異なった形状で今までになかった独特のグリップ感です。
スペック
メーカー VAXEE ツイッター @vaxee_Japan 製品ページ ZYGEN NP-01 形状 左右非対称 長さ 119.7 mm 幅 66.8 mm 高さ 38.9 mm(ソール抜き) 重さ 79 g スイッチ Huano Pinkdot センサー 3389 LOD 1 mm未満 DPI 400(赤) / 800(紫) / 1600(青) / 3200(緑) ポーリング 125/500/1000 Hz ソフトウェア なし 形状
NP01はS2を強調した形状の右側に付け加えた形状。
上下

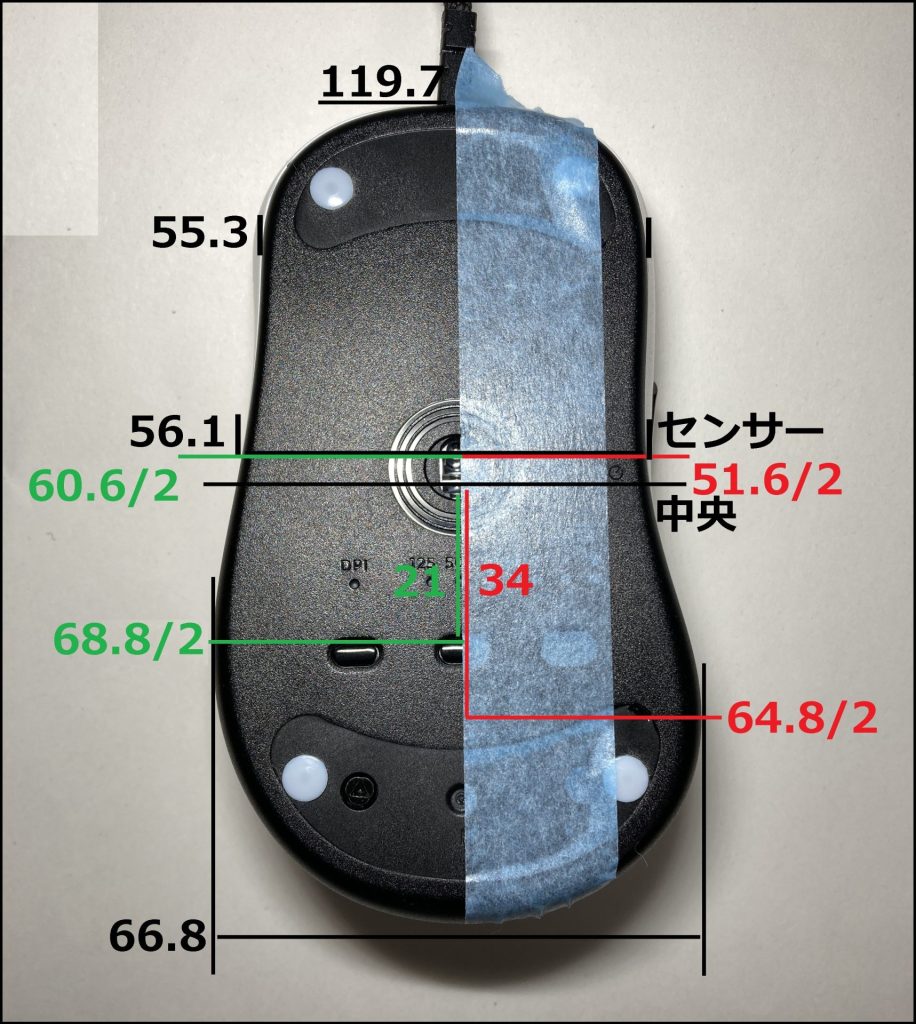

右サイドが膨らんでいる サイズ感
全長的に小型だがやや大きく感じる。
尻
左右尻合わせた最大幅は66.8 mmある。
左側のリアは64.8 mm相当。右側のリアはピークがやや前方に寄り68.8 mm相当。
対称形状の右側に付け加えた感じ。なのでマウスの中心が左にずれて左側もS2より大きく感じる。
くびれ
右サイドの最も細い部分は結構奥めにある。
左右くびれを合わせた最小幅は53.5 mmと対称マウスが元になっているだけあり狭め。
左サイド
センサーあたりで特にくびれており51.6 mm相当。
S2より幅が狭くよりくびれている。
右サイド
右サイドは非対称マウスらしくフロントに向かって細くなっていく。
フロント部分は強めに逆台形になっていてS2より傾斜が強い。
センサー位置
中央から4 mm程度フロント寄りのセンサー。
対称マウスの右側に付け足した形状だがセンサー位置は対称マウスのままなのでややセンサー位置がやや左に寄っている。
横


トップ
NP01のTOPは中央から12 mm程度後方にあります。
38.9 mm。S2より高い。
MB
クリック部分が全体的にフラットな形状。S2より高い。
前後


右側に付け足した形状。
非対称マウスですがトップは傾いておらずチルトグリップを強制されることはない。
特徴
- L 119.7 x W 66.8 x H 38.9 mm
- 対称マウスの右側に付け足した非対称形状
- S2を強調した形状がベースで、S2の右に付け足した形状ではない。
比較

EC2と比べてみる
- センサーが親指側に寄っている
- 左サイドリアのふくらみが大きく、親指付け根にec2より強く当たる
- 右サイドリアのふくらみが急で手前側にも太さがある
中身
分解




ピンアサイン 初期ロットは△ねじTA2であとはTネジらしい
ビルドクオリティ
VAXEEはLogicool G PRO WLみたいな内部にフレームを設ける構造で剛性は良さそう。クリック感もいい感じ。
新型出してPRO X SLみたいに軽量化してほしいところ。
ホイール
24ステップの光学ホイール。回りは重く大きな音がする。
ホイールクリックは普通のチルトタイプじゃなくて直下にスイッチあるタイプ。
押下部にゴムが巻いてあるが取ったほうがホイールクリックはしやすい。多少軽くなるが誤爆しやすくなるので気になるなら戻せばいい。
ばねが付いておりホイールクリックを補助しているらしい。
クリック
スイッチはhuano pinkdot
軽くはっきりしたクリック感でストロークも短い。
ポストトラベルが全然ない
サイドボタン
2つついている。
支障はないがサイドシェル強く握りこむと誤爆する。内部フレームの効果はそこまでなのかもしれない。まあPROWLもサイド押し込むと誤爆するのでこんなもんか。
ケーブル
硬めの疑似パラコード。交換した方がいい。
センサー
いいセンサー
LODは0.65 mmソールで1 mm未満と短い。
純正の薄いやつでないならLowでない方が合うかもしれない。
設定
本体で設定
- DPI:400(赤) / 800(紫) / 1600(青) / 3200(緑)
- 125/500/1000 Hz
- デバウンスタイム:2/4/8 ms
- LOD:Low/ Mid / High
グリップ
重さ
79 gと軽くはない。重心はセンサーあたり。
コーティング
マットコーティング旧新ともに手垢がつきやすい。
つまみ
非対称なのでセンサー傾けて持つと自然に指を配置できる。
つかみかぶせ
S2より親指のくびれが強く右サイドは台形なため平行四辺形な感じにとてもマウスが傾いて感じる。斜め感がkerisみある。
S2と異なる点として右側に盛ってあるので小指の付け根とかにもしっかり接し密着感ある。
既存の対称マウスも非対称マウスもしっくりこなかった人に合う気がする。
トップが傾いてないのでチルトグリップせずに非対称マウス使いたい人に合うかもしれない。
おわり
VAXEEのしっかりとした作りでクオリティは申し分ない。
S2を非対称にした形状と思っていたがS2まんまでなくS2を強調したものがベース。
NP-01は対称マウスとも非対称マウスとも異なる唯一無二な形状で既存のものが合わない人に合うかもしれない。
前の記事:Logicool G PRO HERO マウスレビュー
次の記事:Razer Viper Ultimate マウスレビュー
感想
S2が好きな人には合わないんじゃないかと思っている。そもそもベースがS2をやや大きくし、よりくびれさせ、逆台形を強めた形状なのでS2でちょうどいい人にはくせが強いと感じるかもしれない。がばがば手測定だけどS2強調した形状なのは間違いない。
フィット感を得られる持ち方はできるが小指部分は台形で薬指部分は強く逆台形でそのギャップがどうにも合わず動かしにくいと感じる。
くびれが深いのとマウスの中心がセンサーより左に寄っているので左サイドの出っ張りがS2より主張してきて母指球が痛くなった。
zowie-cシリーズはどうして内部フレーム構造にまでしたのにPRO WL的なトップマウント構造を採用せずビルドクオリティを下げてしまったのか疑問。
VAXEEのマウス構造とかめちゃくちゃいいと思うがnp01とaxはコーティングと形状があまり合わなかった。もっと色々出してほしいな。
-
Logicool G PRO HERO マウスレビュー
Logicool Gの左右対称小型マウスPRO HEROをレビューします。
通称卵、所謂GPRO有線、G102 、G203、G304と同形状のマウスです。
手元のものは型番はG-PPD-001tで新しいモデルとなっています。
G-PPD-001は3366センサーで編組ケーブル、スイッチがOMRON D2FC-F-7N(20M)
G-PPD-001rはheroセンサーになり柔らかいゴムケーブル、スイッチがD2FC-F-K(50M)
G-PPD-001tはスイッチがD2FC-F-7N(G1)と変更されています。
ちなみに002がWLで003がX SL
スペック
メーカー ロジクールG ツイッター @LogicoolG 製品ページ PROゲーミング マウス 形状 左右対称 長さ 116.4 mm 幅 62.2 mm 高さ 37.4 mm(ソール抜き) 重さ 85 g スイッチ D2FC-F-7N(G1) センサー HERO25K 最大速度 400以上 IPS / 85 G LOD 1 mmちょい DPI 150-25.6K(50刻み) ポーリング 125/250/500/1000 Hz ソフトウェア ロジクールG HUB 形状
全長116.4 mmと短い卵型の形状の左右対称マウスです。
上下


サイズ感
ボトム中央の幅が50.4 mmと狭く全長も短い小型マウス。
リア
卵型の形状で尻に幅がない。
ボトム
ボトムは50.4 mmの幅が一定。
トップ
ボトムの幅は変わらず一定ですがトップは中央が最も太くフロントとリアに細くなっていく。
逆台形度
ボトムとトップの形状からわかる通り中央の方が逆台形が強くフロントに向かって弱くなっていますがフロントの逆台形度も6.7 mmと大きい。
センサー位置
センサー位置重心ともに中央。
横

トップ
TOPは中央から15 mm程度後方にあります。
37.4 mmの高さがありなだらかな尻で緩く落ちていく。
MB
ガイドがある平らな感じのMB。
前後


平らなトップ
サイドはやや外側に弧を描いている。
特徴
- L 116.4 x W 50.4-62.2 x H 37.4 mm
- 卵型の形状
- ボトムはフラットで強い逆台形
- なだらかなトップ
- 中央なセンサー位置
比較
中身
分解





ピンアサイン 3 mmと厚みのあるシェル。尻のシェルは単体で13 gあるのでつまみ持ちの人は外すだけで結構軽くなる。
ホイール
kailh製のエンコーダで静かに回りノッチ感がしっかりある。
クリック
スイッチがOMRONのD2FC-F-7N(G1)。古い型番はD2FC-F-Kだったはず。こっちの方がいい感じ。
PRO WLがチャタリング多発しすぎてスイッチが変わった記憶があるが関係なかったっけ。私のはチャタってないのでわからない。
軽く歯切れよくストロークも丁度良く非の打ち所がない。

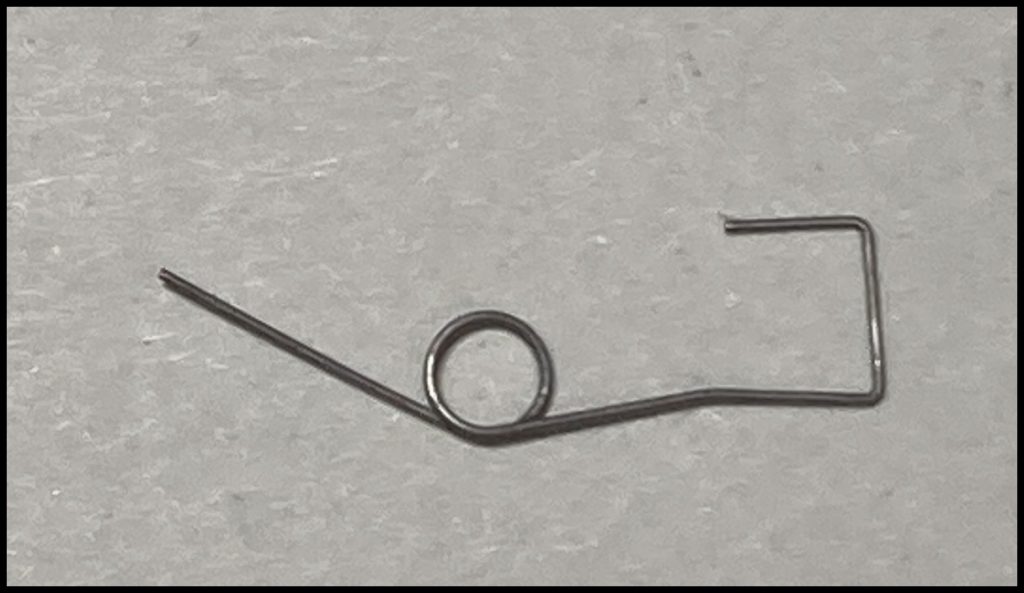
バネが入っており押し下げをアシストしてくれて柔らかく、初動が軽くなり動作点までわずかにストロークが短くなる。
このばねを外すとより歯切れよくなり連打しやすくなると感じた。有り無し試してみるといいと思う。
サイドボタン
サイドボタンがある。
ケーブル
柔らかいので取り回しはいいがパラコードケーブルがあるなら交換した方がいい。
センサー
いい性能。
LODは1~1.5 mmぐらいと短くちょうどいい。
ソフトウェア
Ghubで設定
- DPI:150-25.6K(50刻み、最大5ステージ)
- 125/250/500/1000 Hz
- 6ボタンに自由度のあるボタン割り当てが可能
- テールとロゴ部分にライティング設定可能
- オンボードメモリ(プロファイル5つ)
グリップ
サイドは逆台形が強くやや中心が太いが幅にあまり差はない形状。
ボトムの幅だけでいえば多くの小型マウスよりも細く挟み込みやすい。
くびれがなく指に引っかかりがないので安定感は得にくいが持ち上げやすい。のでグリップテープ等を貼るのもあり。
まっすぐ持つと左右で挟み込むような感じで、センサーを傾けさせて持つと手前に引き付けるように持てる。
重さ
85 gとやや重い。重心は中心で持ち上げやすい。
コーティング
トップはマット、サイドは軽い梨地加工。
つまみ
小型マウスでつまみやすいが重い。
つかみ
持ちやすい。フィット感は得にくいがしっかり動かせる。
おわり
重さはあるがクリック感がよく性能も申し分ない。
5000円帯のマウスでは特に性能ビルドクオリティよく形状合えば買わない手はない。
ぜひ軽量版を公式に出してほしいところだがそんなことはなさそう。
前の記事:[雑記]Logicool G502 3366 感想とか
次の記事:ZYGEN NP-01 マウスレビュー
感想
S2と似ても似つかないのにフィーリング似てるなと思ってたんですがたぶんどちらもフロントの逆台形強いとこが似てて薬指の感じが親近感沸いてたんだろう。
軽量版でないかなあ。
-
[雑記]Logicool G502 3366 感想とか
Logicoolの多ボタン左右非対称ゲーミングマウス G502 3366 を紹介します。
これぞゲーミングマウスというかっこよさがあり無線で性能もいいという、1つのコンセプトとして完成されているように見える G502WL 。
気になりますが気軽に試せる値段でもなくとりあえず試すために中古で G502 3366 を購入しました。
スペック
メーカー LogicoolG ツイッター @LogicoolG 製品 G502 3366 形状 左右非対称 重さ 125 g~(おもり要素) スイッチ OMRON D2FC-F-7N(20M) 割り当て可能数 13 センサー 3366 LOD 1.1 mm, 較正1 mm未満(ソール0.55 mm) DPI 50-12k(50刻み) ポーリング 125/250/500/1000 Hz ソフトウェア ロジクールG HUB 形状
左右非対称のマウスですがIE系とはやや異なるタイプの形状です。
全長130 mmと長そうだがMBの先がとがっている分な気がする。
高さ41 mmぐらい
親指あたりの幅58とか。対称マウスと比べるとやや太いがフロントに行くにつれて細くなっている。


尻は左サイドより右サイドの方が膨らんでいて非対称マウスにありがちな母指球が膨らみにあたって痛いということは起きにくい気がする。まっすぐ持った時の話で斜めにセンサー傾けて持つとまた変わってきそう。
右サイドはフロントに向かって細くなっていく ハ の字。


トップの形状は緩ーく右下がりで軽いチルトグリップを想定していそう。


右サイドは中央あたりは台形だがフロントは逆台形となっている。


右MBは膨らんだ形状で右サイドに向かって曲線を描いて低くなっていく。右サイドとつながるかのようで、中指薬指小指を流れに合わせて持つといいのかもしれない。右MBはトップというより右サイドのパーツというような感じか。
左MBは深めのガイドがある。
分解・組み立て
G502めちゃくちゃパーツ多くて1回目に分解するときは手間取りました。のでその苦労をお届けします。
組み立てなので分解は下から


ホイールをクリアパーツに戻し、黒いカバーのようなパーツをはめ込み裏をねじ止め

ケーブルとブッシュを固定はめ込み、ブッシュ上部にクリアパーツを載せます。
センサー基板を載せスペーサを挟みねじ止めします。

基板を載せ3か所ねじ止め。黄色の丸いホイールクリック脇の穴に小さいネジを入れます。最初分解するときにばねを吹っ飛ばして探すのに苦労してしまいました。
ホイールパーツを固定する黒い部品を基板上に固定します。

ホイールパーツを載せ穴に棒を差し込むことでホイールパーツを固定します。

マグネットをはめ込み、サイドボタン基板を溝にはめます。


サイドボタンを組みネジ止めします。シェルにはめ込みねじ止めします。

シルバーのパーツをはめねじ止め。


クリック横のボタンをはめねじ止めします。

その前のボタンもはめてねじ止め

先に左クリックを固定します。


RGB用のパーツをはめねじ止め、シェルをはめます。


尻部分のシェルを3箇所ねじ止めし、残りのボタンパーツを固定します。
上下合わせてねじ止めし組み立て終わりです。
最初分解したときは結構手間取りました。設計の人は良く考えたもんだと思う。
なくても使えるものではあるがホイール下のばねは初見殺しなので飛ばさないように気を付けたほうがいい。
比較
vs gpwl
サイズは同じぐらい



vs ec1
IE系とは全然違う感じ




中身


ピンアサイン これだけパーツがあれば重いはず。すごい数。
G502 WLでは構造がG PRO WLのように内側にフレームがあるタイプに一新されているのが公式サイトからわかります。この構造で軽量化を図っているらしい。
いろいろ軽量化したとしても元が125 gではいくら頑張っても80 g台にはならないと思うのでだったら重さを楽しんだ方がいいかもしれん。
クリック


メインは20Mのもの、サブボタンは耐久値の低いモデルを使用しています。サブボタンのクリック感もメインに近くていい。
先端部分を押すとロジらしいクリック感があります。スイッチが結構前方に配置されていることからか根元やホイール横あたりを押すとOMRON 20Mにしてはちょっと重め。
ホイール
ホイールはVaxeeやZowie無印モデルのように回すと大きな高い音が鳴ります。光学ホイールです。
ホイールクリックは重いですが左右チルトボタンは軽いです。
ホイールの軸でクリックするホイールクリックでなくホイールを直下に押し込むタイプ。
最近では左右チルトあるわけではないですがRoccatやVaxeeやZowieも直下に押し込む構造ですね。
チルトはこの構造がいいのですかね。チルト無いなら製造コストがかかるだけな気もします。あまり使用感で差がない気がする。
スクロールは大きな音でノッチ感のある回転とフリースピンの2種類で両極端な気もします。
ケーブル
ケーブルは硬いですが本体に重量があるのでどんなケーブルでも何も気になりませんね。
センサー
3366センサーでほぼ文句なし。LODも1 mm未満に設定できて短い。キャリブレーションできる。
ソフトウェア
Ghubで設定を行えます。
DPI、ポーリングレート、ボタン設定、キャリブレーション、ライティングの設定。
ボタン割り当てが13か所にできます。

私はLEDを消しました。ボタン多すぎて逆になに割り振るか困りますが使いこなせたら効率がすごくなりそう。
グリップ
125 gと重いです。現在ラバーをはがしグリップテープ、底面パネルとマグネットを外し110 gです。
重心は中央でセンサーよりちょっと前です。
側面がラバーコーティングというかゴムが貼ってあります。使い始めは良さそうですが汚れや持ち方によってはえぐれていくので私はあまり好きではないですが滑らず弾力もあるでグリップ力はあります。
凹凸のないGPROWLを非対称エルゴノミクスにしたような大きさと形状です。いわゆるIE系の手全体と密着させるような形状ではないです。右側面は軽い台形から軽い逆台形になっています。
右クリックは指のガイドがなく盛り上がっているタイプ、左クリックは指のガイドがありくぼんでいるタイプと左右で異なっています。
左右で指の置き心地が異なりますが、高低差を考慮しての設計だったりするのでしょうか。それとも単純にサブボタンの設計上とかだったりするのでしょうか。
かぶせ
サイズ的にも非対称な形状からもかぶせ持ちにあっています。フロント部は軽い逆台形になっているので左右非対称の中で持ち上げやすい部類です。GPROWLをエルゴライクに持っている人にははまりそう。
つかみ
右側面が非対称マウスとしてはフラットな部類で非対称としては幅が細め。
クリック部は左が高く右が低い形状ですが尻の部分は軽微な右下がりで非対称ですがチルトグリップでなくとも手のひらに違和感はなく持ちやすい部類です。
小指がまげて中央あたりに配置すると側面がやや台形で、伸ばして奥めに配置すると逆台形なのでグリップ感が異なる。
つまみ
ホイール位置がちょっと後ろめだからかもしれませんが最初にぱっと持ってみてくださいと言われたらつまみ持ちで持つ気がします。
MBが高めなこともありわしづかみというよりは指を伸ばし気味なつまみ持ちがしやすいです。
おわり
他にはない特徴的な形状で面白いですね。RazerのBasiliskが似たような形状らしいです。
多ボタンでフリースピンもついておりギミックが凝っていますがホイールは重いか軽いかの両極端でバランスが悪い気もします。重いですが性能高くFPSで使えますし、多ボタンなので作業用にもいい。
重めのマウスを使いたいときに90 gのマウスとかでもいいですが100 g越えと振り切っているg502の方が使っていて楽しいし重さを活かしたエイムができる気がします。重さが欲しいときはg502一択でいいんじゃないかと思った。性能いいし形状も特徴はありますが持ちやすいし。
試しにG502を買ってみて無線版を買うか?という話題でしたが欲しい!
前の記事:Zowie S1-C マウスレビュー
-
[自キ]手配線でホットスワップ対応のキーボードを作る
手配線でホットスワップキーボードができないかと思い試しに作ってみました。自キ制作レポートです。
設計方針
前回の分割キーボード制作で手配線のやり方は自分の中で結構納得がいったので手配線でホットスワップ対応のキーボードが作れないかと思い試作してみることにしました。
手配線でホットスワップというとミルマックスが思い浮かびそうですがkailhソケットで作りました。こちらの方が安いし簡単だと思ったので。
出来上がり

4キーなのもあってぱっとできました。
考え足りずソケットむき出しで抜くときに引っ張られてしまったためボンドで固定しました。
キーキャップを引き抜くとスイッチごと抜けてしまうのでトッププレートはきつく設計する必要があるかもしれません。キーキャップ交換しないのならこれでもいい気がします。
アクリル積層は打鍵感は硬いですが打鍵音は結構いい感じなんですね。

次作るときは4層にして部品を押さえればよさそう。
材料
アクリルカット
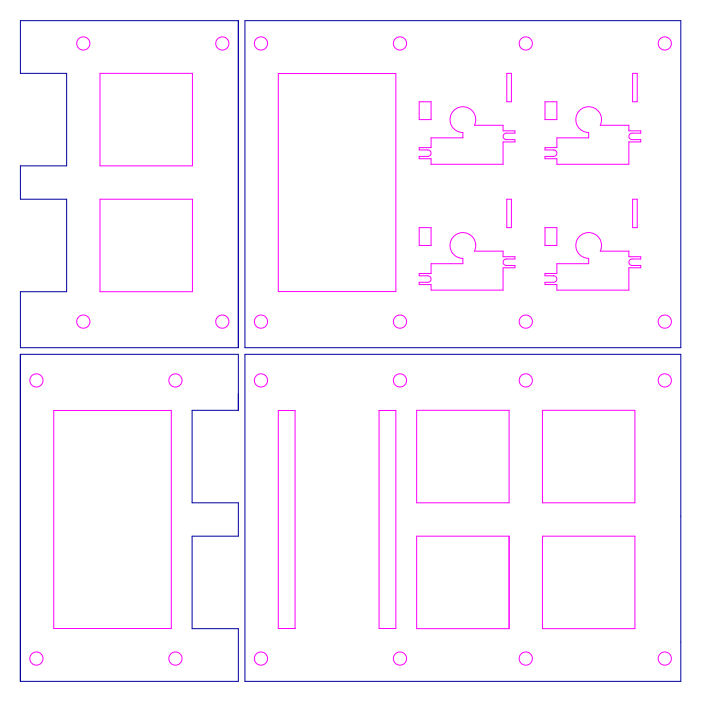
参考:スイッチ用PCBソケット(10個入り) – 遊舎工房 (yushakobo.jp)データシート
参考:Kailh BOX スイッチ(10個) – 遊舎工房 (yushakobo.jp)データシート
Acrylic Laser Cutting – Order Online (elecrow.com)にて2.5 mmのアクリルカットを注文した。
試しだったので最小サイズの10×10で収まるように。
3層アクリルプレート。上2枚はキースイッチ用の四角い穴でボトムプレートとの間にはナットを挟む。
ボトムプレートはキースイッチの足、kailhソケット、ダイオード固定用の穴をあけた。
思い立ったが吉日さっと書いたのでソケット固定できていなかったりと残念な点が多い。立体を頭の中でうまく組み立てられていない気がする。
組み立て
アクリルプレート

アクリルプレートが届きました。かわいい?キーホルダー付きです。

こんな感じで3層になります。
kailhソケット


こんな風になってるんですね。シンプルだけど実用的で偉大そう。

ボトムプレートにソケットを乗っけます。きれいにはまってくれてよかったです。
はんだ付け部分を2か所引っかけているだけなのでぐらつきます。
配線

ダイオードとワイヤーを配線しました。アクリルに乗っけてはんだ付けするだけなので簡単です。
組み立て

トッププレートを。ネジ止め。2枚重ねてナットで締めます。

ボトムプレートもネジに差し込みねじ止め。
promicroを上からはめ下からはんだ付け。

上から見てソケット丸出しなことにこのときやっと気づきました。図面書いてた時にはソケット上に1枚あると思い込んでいたんです。
キースイッチ

スイッチを挿してみました。ソケットにぶっ刺さってる。
このままだと抜くときにソケットが上に引っ張られるのでボンドでソケットを固定しました。
完成

ボンドが汚いですが無事完成。
余分なねじを切り落としてゴム足付ければそれっぽくマクロパッドとして。
反省点
手配線でホットスワップのキーボードを自作することができることを確認した。
利点はpcbを設計しなくていいこと、配線が透けて見えてなんかいい感じなことです。
欠点はpcb設計すればそれで済むじゃん。
アクリル4層にすれば今回問題となったソケットの固定はクリアすることがでる。その場合上は5 mmを1枚もしくは2.5 mmを2枚だろうか。下2枚はできるだけ薄い方がよく2 mmを2枚になりそう。厚みは1cm+ゴム足ぐらい。
できれば1.6 mmとかがいいですが、となるとFR4なのでpcbを設計しろの一言に尽きる。手配線でキーボード作るのは完全に工作趣味でしかない気がします。pcbの方が安上がりだし。
また今回promicroをめんどくさいやり方でつけましたがpromicroは裏側に張り付けて配線できそうです。今回の場合そうすれば厚みはその分増しますが10×10サイズで6キーのマクロパッドができそう。
あとは配線用にもっと細い単線のワイヤとか用意しておけばやりやすそう。
10×10のサイズで気軽にいろいろ試してみるのは面白いかもしれない。でも試すだけならブレッドボード使った方がいいじゃん。
いい加減pcb設計しろ
前の記事:[雑記]PulsarGamingGears メカニカルスイッチテスター
次の記事:[雑記]TALPKEYBOARD Gateron CAP キースイッチセット 比較














![[自作マウス]op1 8k v2 基板採寸](https://tsuiha.com/wp-content/uploads/2025/12/image-12.png)

![[BF6]視野角と感度の設定について](https://tsuiha.com/wp-content/uploads/2025/10/image-36-3.jpg)
![[自キ]KS-33B Gateron LowProfile 3.0スイッチに希望はあるのか](https://tsuiha.com/wp-content/uploads/2025/09/IMG_3528.jpg)
![[自キ]チルトテントアルミケースな左手デバイス作る③修正](https://tsuiha.com/wp-content/uploads/2025/09/image-2.png)
![[自キ]チルトテントアルミケースな左手デバイス作る②ケース](https://tsuiha.com/wp-content/uploads/2025/08/image-26.jpg)
![[自キ]チルトテントアルミケースな左手デバイス作る①基板](https://tsuiha.com/wp-content/uploads/2025/08/image-24.jpg)


![[自キ]遊舎工房のレーザー加工サービス利用してみた](https://tsuiha.com/wp-content/uploads/2025/08/image-5-1.jpg)


![[自キ]磁気キーボードを作りたい。6週目](https://tsuiha.com/wp-content/uploads/2025/07/image-2.jpg)

![[自キ]磁気キーボードを作りたい。5週目](https://tsuiha.com/wp-content/uploads/2025/06/image-27.jpg)

![[自キ]磁気キーボードを作りたい。3週目](https://tsuiha.com/wp-content/uploads/2025/05/image-15-1.jpg)
![[自キ]磁気キーボードを作りたい。2週目](https://tsuiha.com/wp-content/uploads/2025/05/image-9.jpg)
![[自キ]磁気キーボードを作りたい。1週目](https://tsuiha.com/wp-content/uploads/2025/04/image-25-1.jpg)
![[自キ]50%オーソリニアのキーボード作った OSPREY59O](https://tsuiha.com/wp-content/uploads/2025/03/IMG_2343.jpg)






![[自作マウス]haste2基板を3Dモデルに起こした](https://tsuiha.com/wp-content/uploads/2025/01/image-10.jpg)

![[デスク]VESA拡張してモニターを増設した](https://tsuiha.com/wp-content/uploads/2025/01/IMG_2567.jpg)
![[デスク]充電ケーブルを天板裏に移動してすっきりした](https://tsuiha.com/wp-content/uploads/2025/01/IMG_2565.jpg)

![[自作マウス]マウスシェルモデリング その2](https://tsuiha.com/wp-content/uploads/2024/11/IMG_2288.jpg)

![[イヤホン]moondrop 水月雨 KadenzとKatoの雑話](https://tsuiha.com/wp-content/uploads/2024/11/IMG_2385.jpg)

![[オーディオ]ジェネリックER-4B化モジュールを作る②](https://tsuiha.com/wp-content/uploads/2024/08/er4switch1.jpg)
