- Home
- 一覧
-
ZOWIE EC1 & EC2を比較 マウスレビュー
ZOWIEから発売されている左右非対称マウス EC1-B と EC2-B divina を比較して紹介します。
ECシリーズは尻がなだらかなタイプのエルゴノミクスマウスです。
スペック
メーカー BenQ ZOWIE JapanHome ツイッター @ZOWIE_eSport_JP 製品 EC1 EC2 形状 非対称 長さ mm 128.4 122 幅 mm 70.5 65.9 高さ mm(ソール抜き) 42.1 42.1 重さ g 96 92 スイッチ Huano Bluedot センサー 3360 LOD 1.2 mm DPI 400 / 800 / 1600 / 3200 ポーリング 125/500/1000 Hz ソフトウェア なし 形状
上下




サイズ感
EC2は全長122 mmと中型、EC1は全長128.4 mmと大型なサイズ感
リア
やや右サイドに寄っているエルゴマウスらしい感じ。
左右合わせた最大幅がEC1は70.5 mm、EC2は65.9 mmある。
くびれ
最小幅はEC1は58.9 mm、EC2は54.9 mmある。
左サイド
左サイドピークからまっすぐくびれていき ハ の字になっていて親指がフィット感を得やすくなっている。
右サイド
手のひらに合わせたふくらみがある。
やや前方には小指の位置にフィットするくびれがありその先に薬指を置くふくらみがある。
深く持つ際は関係ない。
センサー位置
ホイール位置を中央とするとセンサーは右側に2.5ほど寄っている。
センサー位置はEC1は中央から5 mm、EC2は3 mm程度フロント寄り。
横






トップ
TOPは中央でどちらもおなじ42.1 mmある。
尻は結構なだらかな感じ
MB
左右で高低差のあるクリック部で指先にフィット感を得られるガイドがある。
深く持つときは関係ないが。
前後




かなりチルトグリップな感じ。
右サイドは全体的に台形で持ち上げる際の引っかかりはない。
ここがIE形状との差でIEはフロント部分はやや逆台形になっている。
また右サイドの傾斜もECの方が急になっている。
特徴
- EC1、EC2ともに高さは同じで水平方向にサイズが異なる
- トップは中央で高め、なだらかな尻な左右非対称形状
- 指先に合わせたガイドがありフィット感を得やすい形状だが深く持つと関係ない
- 左高右低のチルトグリップな形状




比較
中身
分解




ピンアサイン 二段重ねになっているPCB。分厚いシェル。
ホイール
光学式ホイールで重くうるさい。
クリック
スイッチはHuano BlueDot。
一体型のMBで押下部は後方寄りとなっている。
MBをしならせながら押し込むようなEC独特のクリック感で詰まった感じ。
divinaの方が柔らかく詰まり感は小さいが、歯切れ悪くふにゃふにゃしならせる感が強い。
ZOWIE感ありポストトラベルが大きい。
指を立てると浮いた感じでガイドに合わせ指を寝かせる方が好き。
サイドボタン
ストロークが長い。
ケーブル
交換
センサー
3360で問題はなかった。
LODは1 mmちょいでいい感じ。
ソフトウェア
本体で設定
- DPI:400 / 800 / 1600 / 3200
- 125/500/1000 Hz
グリップ
重さ
重い。EC-Cシリーズが欲しい。Cシリーズは構造が異なっていてクリック感が異なりそう。
重心はセンサー位置
つまみ
重いし右形状が台形なので持ち上げられない。つまむならIEに近い右サイドの方がよさそう。
つかみ
右サイドが台形なので指の側面でグリップできずわしづかみするのがよさそう。
やや斜めなグリップになるがフィット感がある。
かぶせ
指のガイドがあるので自然に持ててフィット感が得られる。左右で挟んで指先で操作する感じがある。
ガイドを無視して深く持つのも合うと思う。手前に引きやすい。
おわり
各指にガイドがありフィット感があって持ちやすい定番の左右非対称マウス。
合う合わないあるけど非対称マウスはまずEC2試してほしいなと思える面白い形状。
EC1はでかくて指先にうまく力が入らないと思った。手のひら全部に密着感ほしい人向けな感じ。
クリック感は一体型MBの悪いところが出てる感じがあるがdivinaはすごいしなって逆に面白い。
重い。Cシリーズで超大幅減量してるのでわざと重くしていたのだろうけど重すぎる。
前の記事:Zowie FK2-B マウスレビュー
-
FPSに適したマウスのDPI・自分好みなDPIの探し方
FPSにおいてマウスのDPIをどう選択するのかというのは、実際に試して感触よかったりパフォーマンスが出たものを使用するのがベストだと思います。
じゃあなんでもいいのかというとそうではなく、選ぶべきでないDPI値が確かにある。
DPI小さくしたらカーソルがガクガクになりますし、大きくしたら遅延が発生します。
というのが通説というか体感でもそうですしよく知られています。
という前置きの後に、個人的にDPIの違いが分かりやすいなと思ったDPIの選び方を紹介します。
前置き
低すぎるとガクガクする
極端な例ですがDPIを50に設定するとマウスカーソルが動き出すまでに必要なマウス移動距離は、インチをDPIで割って25.4/50=0.5mm程度。
雑に言えば0.5 mm刻みの方眼用紙の上でマウスを動かすようなもので、0.5mm角を最小単位にしていたらそれはカクつくというのは想像に難くないです。
それだけでなく、低いDPIではよりゲーム内感度を高く設定する必要がありますから、そこでさらに倍率を掛け引き延ばされることでよりカクつきます。
ゲームプレイに影響はそこまでないと思いますが、ゆっくり動かせば400 DPIはマウスカーソルに少しだけカクつきが見えることは簡単に確認ができます。
50 DPIで動かすとガタガタとカーソルが動くのがわかると思います。
これは一方で低dpiは直線補正がかかって操作しやすいといわれる話に関わっています。高dpiは手振れがという人がいますがどれだけ高周波で振動してるんだあなたの手はという話で、というよりは低dpiに直線補正があると言うほうが正しいです。
しかし高FPSでポーリングレート125Hzでプレイする人も世の中にはいますからそこまでダメだということでもなく、気になるならカクつかない程度の設定を行えばよいと思います。
低dpiはピクセルスキップがという話もありますが、実際に検証してみるとピクセルスキップが起きるのは超ハイセンシという特殊な場合でしかないです。
しかもdpi由来というよりはゲーム内感度が高くなりすぎる引き延ばし効果によるため、理論上は問題でも実際は考慮する必要がないことが分かります。
高すぎると遅延する
スムージングについては以下のredditを見てください。DPIが高いとスムージングがかかるようになっておりその分latencyが発生するみたい。
3370はスムージングがないみたいです。
ほんとかよと思う人もいると思うので適当に確認してみます。3389のburst proと3370のkone proで比べてみます。
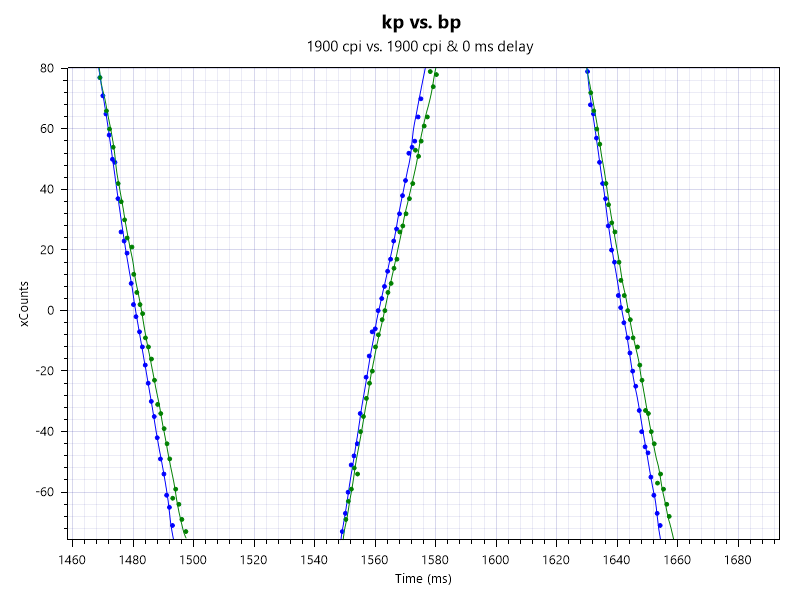
1900dpiでbp(緑)がkp(青)に比べ明らかに遅れています。
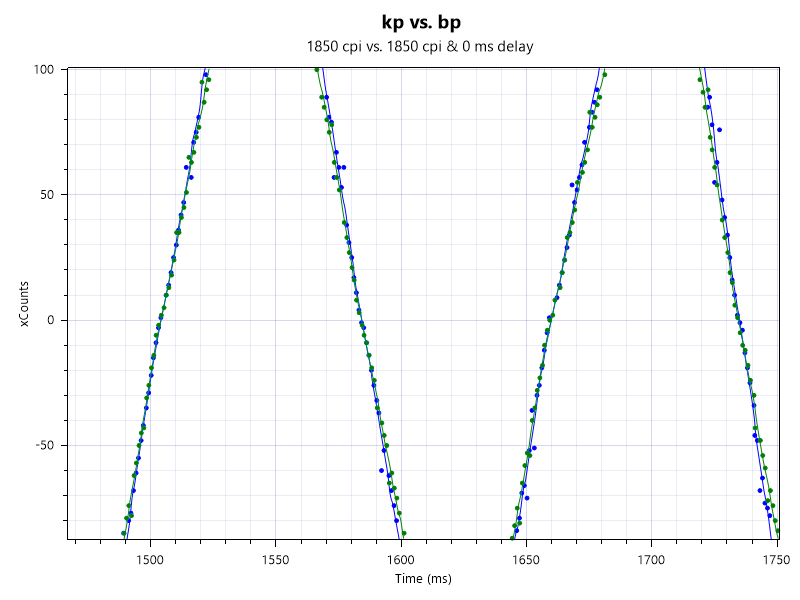
1850dpiでは差はなさそうです。redditと同じ結果を得られました。詳しい人が書いているのだろうからそりゃそうなんだけども。
というわけで3366や3370は例外のようですが、基本的にdpiは高くても1800~2000あたりがよさそうですね。
DPIの分解能を感じる
結局のところDPIは400-1600あたりがいいらしい。3370なら高くてもいいらしい。
じゃあ400と1600どっちがいいのか800がいいのかって話です。
dpiの違いはその定義通り分解能でしかありませんが、実際にその違いを体感することができれば好みなdpiを選択することができます。
わかりやすくDPIの違いを体感できるのはこれがいいんじゃないかなと思いました。
GitHub – RawAccelOfficial/rawaccel: kernel mode mouse accelkernel mode mouse accel. Contribute to RawAccelOfficial/rawaccel development by creating an account on GitHub.マウス加速ツールrawaccelを入れます。ダウンロードしてインストーラダブルクリックして再起動するだけです。
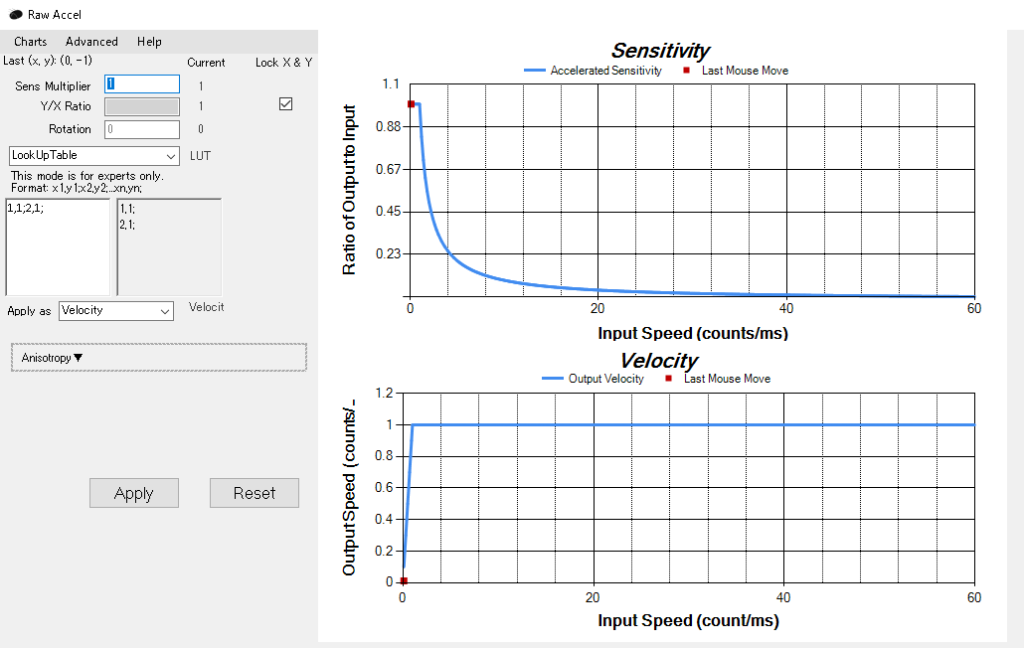
このように設定するとvelocity、マウスを動かす量にかかわらずカーソル移動速度が一定になります。パッドのジョイスティックとか、マウスカーソルをキーボードで動かすような感じ。
DPI切り替えながらマウス振ってるとなんとなく違う。動き出しとか止まりとかぬる感とか。
DPIが高い方が繊細で動き出す最小値が小さく追従性がよりリアルなことがわかります。DPIが小さい方が大雑把で閾値が大きいことがわかります。
数十マイクロメートルの単位ですが案外体感できるのがわかると思います。
19kに設定するとすごいカーソルが動きやすいです。1 umですものね19kは。
低DPIは高DPIと比べて遅延する?
先述したスムージングとは別の話。よく1600dpiは400dpiより遅延が少ないといわれています。
どちらが手の動きに対して遅延が少ないですか?と聞かれたら1600dpiだと私は考えます。
しかしその遅延というのは有線と無線マウス、デバウンス有りと無し、のような絶対的なXX秒の遅延差がある、といった状況とは異なっています。
挙動を比較してみる
例としてマウステスターで高DPIと低DPIとでマウスをスッと動かしてからスッと止めてみます。
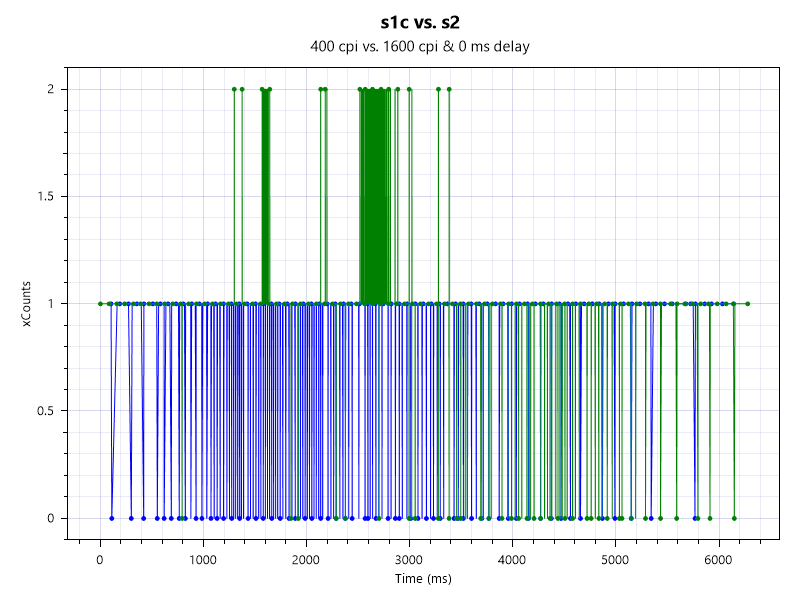
青が400dpiで緑が1600dpiです。マウスを動かし始めて止まるまでのデータです。左端(マウスの動き始め)と右端の(マウスの止まる部分)とを見てみると、
緑動く→青動く→青止まる→緑止まるとなっていることが分かります。
つまり低dpiは初動の送信されるのがやや遅れるが、高dpiは手でマウスを完全に止めるまで検知し続けるというのが分かります。
youtubeなどで海外の400dpiは入力遅延がという検証ありますが、これは入力遅延ではなくdpiによる特性です。(スムージング有りと無しのような)絶対量の入力遅延があるのであれば、止まるのも400dpiが遅いはずです。
この例では1600dpiより400dpiが早く止まっています。これはよくいう遅延というより単に分解能の違いによる性質です。
ああいうのを何も考えず鵜吞みにするのは良くないですよ自分の頭で考えてください。dpiがドット・パー・インチであるということでしかないのですから。
高dpiと低dpi
高DPIのほうがよりアナログな手の動きに近しい正確さを持ちまた反応が早いですが、固定でXX秒遅れるというわけでもなく、絶対量として入力遅延があると考えることには違和感があります。一般的に遅延というとこちらを指すように思い、「高dpiは遅延が少ない」と端的に言ってしまうと誤解を生む恐れがあります。
実際DPIが高いほうが遅延ばらつきが小さく高DPIの方が画面のぬるぬる感が強いですしそういった点において1600DPIが強いと感じます。
では低DPIにはメリットはないのでしょうか。高DPIの方が反応が早いですし性能面においてメリットはないように思えます。
遅延があるといわれる所以ではありますが、1600dpiカーソル移動量4countsのとき、400dpiは1countsしか移動しません。
つまり1600dpiが1counts移動したときに400dpiは0.25countsで1に満たず、pcにデータは送信されません。
イメージとして低dpiは移動量をため込み一定値を超えると通信します。1600と400であればその閾値が4倍大きいわけです。よって低dpiはその意味でもぬるぬる感が弱くシンプルな動きをします。ゲームでなくpc作業だと微細な動きを拾われないため低dpiのほうが快適です。
先ほど画像で示したように、低DPIでは1フレーム分停止が早いという話をしました。このことからマウスを早く振った後に1フレーム早く画面を認識することができるというのはメリットといえるのではないでしょうか。エイム論にはフリックはトラッキングの連続であるという主張もありますが、実際人の目は視線をフリックした際その間の映像を認識しません(サッケード抑制)。
、、、こじつけな気もします。まあ1600DPIが無難でトレーニングにもよいのではないでしょうか。
私は経験上インゲームは400dpi(低)が、エイムゲームは1600dpi(高)が好みでありパフォーマンスも発揮できます。人にもよるのでしょうけど。
おわり
特にこだわりがなければ1600dpiが良いのではないでしょうか。実際操作感が異なるので低DPIのほうが強い・好みということもあると思いますし、こだわりを持つことは良いことだと思います。
他にも謎に言われるハイセンシは高dpiでローセンシは低dpiがいいとか試してみましたがよくわかりませんでした言葉遊びな気がします。
結局dpiの違いはdpiがドットパーインチであることでしかないのですよね。簡単に考えましょう。
快適なマウスライフを
-
Zowie FK2-B マウスレビュー
ZOWIEから発売されている小型対称マウスFK2-Bをレビューします。
スペック
メーカー BenQ ZOWIE Japan ツイッター @ZOWIE_eSport_JP 製品ページ FK2-B ゲーミングマウス for esports 形状 対称 長さ 127.6 mm 幅 64.3 mm 高さ 36.3 mm(ソール抜き) 重さ 84 g スイッチ Huano Blue dot センサー 3360 LOD 1.2 mm(純正ソール) DPI 400/800/1600/3200 ポーリング 125/500/1000 Hz ソフトウェア なし 形状
ブッシュを上に向かせる部分でFK2無印よりやや長くなっていますが形状は同一です。
上下


サイズ感
127.6 mmありますが平べったい形状なので小型マウスに感じます。
リア
尻の幅は64.3 mでスリムであまり深くありません。
中央
くびれは中央から7 mm程度フロントにあり54.1 mmとやや細め。
フロント
フロント部は56.1 mmまで2 mmと中程度広がっていきます。
逆台形度
くびれ部分は4.8 mm、フロント部分は4.1 mm程度逆台形となっていて大きめです。
センサー位置
センサー位置はくびれ当たりにあり7 mm程度フロント寄り。
横

トップ
TOPは大体中央にあります。36.3 mmと全長に対して低い。
なだらかな尻。
MB
クリック部分に軽くガイドがあるやや低めのMB。
前後


台形なシルエット
特徴
- L 127.6 x W 54.1-64.3 x H 36.3 mm
- 全長に対して低く細めの形状。
- なだらかな尻。
比較
中身
分解


ピンアサイン センサー基板はボトムマウント、サイドスイッチ、メインスイッチがトップマウントです。
シンプルで分厚い感じ。重量感があり高級な感じがする。
ホイール
光学式で重いいつものやつ。
クリック
スイッチが横に配置してあり押下部分もだいぶフロントにある。意図的だがなんでだ 。
huano blue dotでzowieな感じだが他のモデルと比べ重いクリック感。
スイッチ直上を押す感じなので押す感じは直感的かもしれない。
FK2無印の詰まった感じは多少改善している。
サイドボタン
低いマウスだがサイドボタンも狭めなのでそこまで干渉しない。
ケーブル
交換するのが良い
センサー
3360で普通にいい感じ。
LODは1.2 mmといい感じ。
ソフトウェア
本体で設定
- DPI:400/800/1600/3200
- 125/500/1000 Hz
グリップ
fk2は出っ張りのないなだらかで薄い自由度の高い形状で薬指もトップに乗せる1・3・1とか人差し指を左サイドに置く2・2・1とかのキメラ持ちがしやすい気がする。
重さ
84 gと軽くはない。ちょい重い。
コーティング
跡が付きやすいマット
かぶせ
低く細いので窮屈。尻は低くなだらかなので自由度はありかぶせライクに持てる。
つまみ
長めだが薄いので手のひらに干渉せず持てる。
でもつまむならmodelO-でよくね感もある。
つかみ
つかみやすいが尻が低くなだらかで細いので手のひらにグリップ感はあまりなく指で動かしやすいタイプ。
おわり
FKは他のZOWIEマウスに比べるとクリック感が重めなクリック感。
全長は中型程度あるが低く細めの形状で出っ張りがなく自由度の高い形状をしている。なだらかな尻は手のひらにグリップ感は得にくい。
結構多い幅や高さは普通で短い小型マウスとは逆の高さ、幅を抑えた全長は普通の小型マウス。
FK2-Bは重いと感じる人も多そう。他のと異なりCシリーズでも構造があまり変わってないので軽くなったCシリーズを買えばいいと思う。
フロントが広くくびれが大きいViperや中央からフロントまで幅があまり変わらないModelOその他FKクローンは多くあるので本家にこだわることもないかもしれないが。
次の記事:ZOWIE EC1 & EC2を比較 マウスレビュー
-
Roccat KONE PRO マウスレビュー
ROCCATから発売されている「KONE」シリーズは左サイドにヘコみがあり、非対称と対称の中間のような特徴的な形状をしています。
左右非対称の軽量中型ゲーミングマウス KONE PRO をレビューします。
今回紹介するのは有線モデルですが同形状の無線モデル KONE PRO AIR も発売されています。
スペック
メーカー ROCCAT ツイッター @ROCCAT 製品ページ ROCCAT® Kone Pro 形状 非対称 長さ 125 mm 幅 72.1 mm 高さ 40 mm(ソール0.6 mm抜き) 重さ 65 g スイッチ Titan Switch Optical センサー Owl-Eye 19K LOD 1 mm(較正で1 mm未満) DPI 50-19K(50刻み) ポーリング 125/250/500/1000 Hz ソフトウェア ROCCAT® SWARM 形状
上下

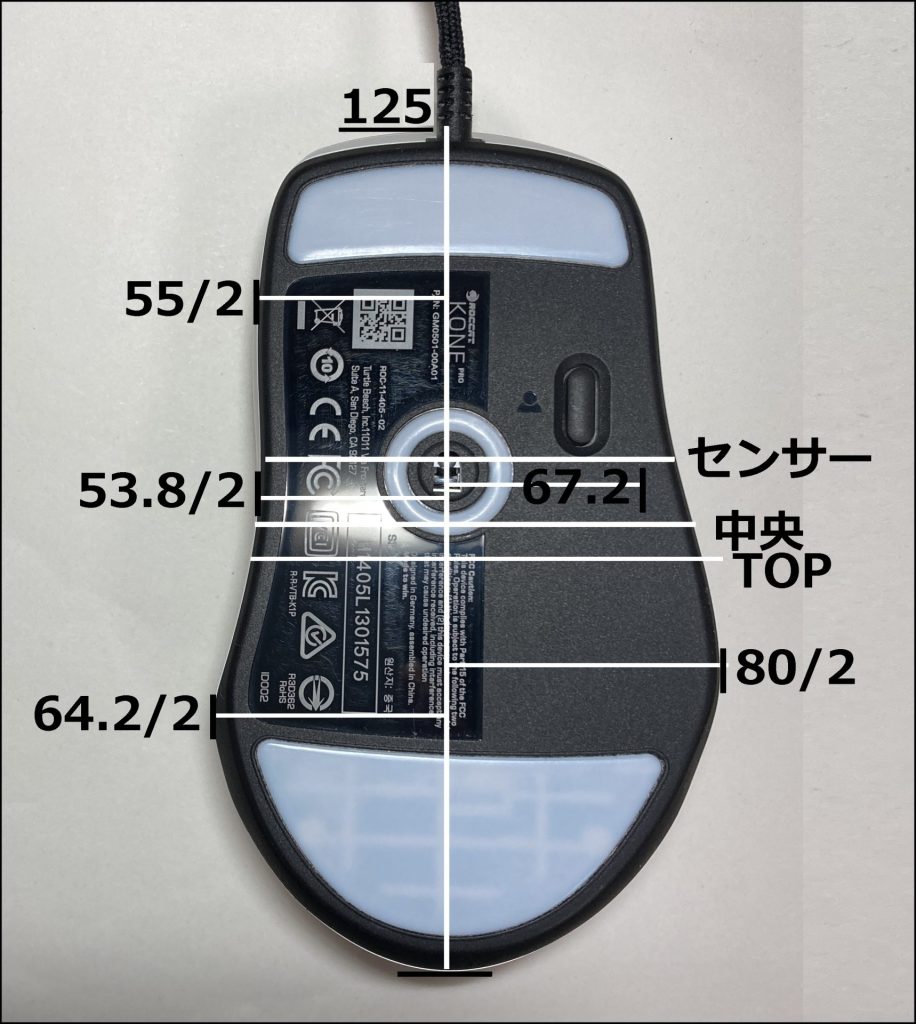
サイズ感
全長125 mmで中型マウス。ホイールが後ろめなのでホイール基準に持つと全長ほど長く感じない。
尻
尻は丸い形状ではなく下に尖ったような三角形な形状で深く持ちやすい。これにより母指球、小指球がシェルの後部に圧迫されず持つことができる。
左右尻合わせた最大幅は72.1 mmあり非対称マウスですが幅のピークは右サイドが手前側に左サイドが奥側にある。
くびれ
左右くびれとも中央あたりにあり、左右くびれ合わせた最小幅は60.5 mm
左サイド
左サイドピークは中央から29.2 mm程度後方にあり80 mm相当ありますが親指のくぼみがあるのでそこまで太くは感じない。
中央から5 mm程度前方の親指位置は67.2 mm相当で親指を置くガイドが掘られていて前後には割とフラット。
右サイド
右サイドピークは中央から20.7 mm
くびれている部分は中央から3 mm程度フロント寄りにあり53.8 mm相当で緩やかにカーブを描きながらくぼんでいる。
フロントにかけて55 mm相当まで再び広がっていき、終端では丸まっている波打つ形状
中央部分フロント部分で幅にそこまで変化は大きくない。逆台形な感じもなく鉛直でフラット。
センサー位置
中央から10 mm程度フロント寄りのセンサー。トップは中央から4 mm程度リア寄り。
横


トップ
TOPは中央から4 mm程度後方にあり尻は出っ張っているがトップは中央寄り。
MB
クリック部分にガイドはなくそのままな感じ。左右で高さが異なる。




前後


カクカクしたなだらかにチルトグリップなシルエット
特徴
- L 125 x W 72.1 x H 40 mm
- 尻はとがっており深く持っても邪魔になりにくい
- 親指のガイドが深く掘られている
- 縦にフラットで波打った形状な右サイド




比較
中身
分解




ピンアサイン サイドスイッチ外さないと内部フレーム分離できず固定されている。MB裏がハニカムな感じ。フレーム構造だからかシェルはのっぺりしている。
ROCCAT® BIONIC SHELL
Kone Pro の堅牢でありながら軽量なハニカム構造はホコリや汚れに強く、66g という究極の軽さを実現。メインクリックの半透明フェードは、鮮やかな AIMO 1680 万色の RGB ライティングを引き立たせます。
ROCCAT® Kone Pro 軽量光学式エルゴノミック パフォーマンス ゲーミングマウスなんでクリック裏だけハニカムなんだろ。
剛性

内部フレームあるのはG PRO WLやVAXEEと同じだがKONE PROはフレームがPCBマウント。トップシェルと何か所かはまって強固にしている感じ。
しかしクリック部分とかフロント部分はスカスカ。
PROWLとかNP01は強く握りこむとサイドスイッチ押されるけどKONEPROは誤爆しないのでこの点は勝ってるかも。何に勝っているのかはわからない。
中央部分はフレームがあっていいかもしれないがフロント部分はフレームないのでかなり柔らかい。ので置いた薬指の力だけでも結構ゆがむ。
ホイール

TITAN WHEEL PRO
アルミニウムから削り出された Titan Wheel Pro は、ROCCAT® の精密なエンジニアリングの賜物です。軽量でありながら頑丈な Titan Wheel Pro は、しっかりした反応のスクロールとクリックとなっています。合金は指の温度に素早く馴染み、非常に快適で臨場感あふれるゲームプレイを楽しめます。
ROCCAT® Kone Pro 軽量光学式エルゴノミック パフォーマンス ゲーミングマウスTITAN WHEEL PROはアルミ削り出しで軽量で頑丈なのがウリなんだとか。
重さ測ってみると2.8 gなので「軽量」というのは金属製としては軽量という意味であり樹脂製のホイールとまったく同等の重さである。
エンコーダはTTC製のやつで軽めの回し心地。
ホイールクリックはチルトタイプじゃなくて下に押し込むやつで軽めだが誤爆しやすい感じ。
アルミ製の利点はいまいちわからないけど謎のこだわり要素男のロマンということで。爪が当たると嫌な感じよねアルミだから。
クリック
スイッチはTitan Switch Opticalでオプティカルらしく重く反発が弱くポストトラベルが大きい。
セパレートタイプのMBで一体型のBURSTよりは歯切れ良い感じかもしれない。

MBパーツだが固定部分の高さが異なるのがわかる。右クリックの方が固定部とクリック部とで高低差が大きい。その所為で押し下げにくく詰まったクリック感になっていて右があまりによくない。
左クリックはある程度の歯切れよさがありクリスピーさがあり悪くないかもしれない。メカニカルスイッチのKPUと比べればこちらの左クリックの方がクリック感はいいし、クリック感の悪いメカニカルスイッチを採用したものと比べればKONE PROのクリック感は普通と言っていいだろう。
サイドボタン
ふたつついている
ソール
熱処理ピュア PTFE グライドで滑りがいい感じ
エッジ処理されているのはいいが淵がわずかに盛り上がってしまっているのであまり大ソール感を感じなかった。布パッドだと気にするほどではないかもしれない。
ケーブル
コネクタが一般的なやつじゃなくて一回り小さいやつなので交換するのに注意。
市販のパラコードケーブルと比べると、細く軽いが芯があり硬め。個人的には好み。
センサー
Owl-Eye 19Kは3370カスタムで普通にいい性能をしていた。
Owl-Eye 19Kは3370のカスタムセンサーで、3370は3389よりエラーレートが下がった改善版らしい。
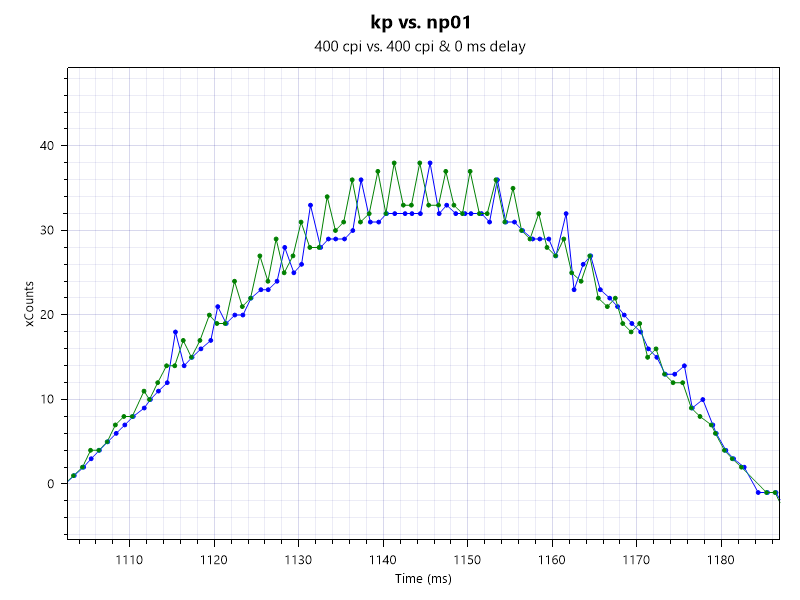
青がKPで3389のnp01と比べてみた。ギザギザが立つ頻度が半分以下に減っているがここら辺が改善されたところなのかもしれない。
そもそもこのギザギザは何なんだ詳しくないので知らない
LODは1 mmといい感じ。較正すれば1 mm未満にできるがmousetester波形が荒ぶりまくったりしたので環境によっては較正を使わない方がいいかもしれない。
ソフトウェア
SWARMで設定
- DPI:50-19K(50刻み、最大5ステージ)
- 125/250/500/1000 Hz
- 底面ボタン含め8ボタンに自由度のあるボタン割り当てが可能。上下ホイールも割り当て可能
- LOD設定
- デバウンスタイム
- クリック部分にライティング設定可能
- オンボードメモリ(プロファイル5つ)
今更ながらデバウンスタイムの設定あるのか。デバウンス遅延のない云々とは。それともサイドスイッチとかの話?
グリップ
KPUと比べるともうちょっと指とか手のひらをゆったりさせて持てる感じでKPUで窮屈だと感じている人には合うかも。
非対称だがそこまでチルトグリップよりではない。軽いチルトグリップに合う傾斜。
重さ
65 gと軽い。重心はセンサーあたり。無線版はもうちょい重くなる。
コーティング
マット加工で手汗全かかないる感じ。
左右サイドは横方向にスリットが入っている。
かぶせ
斜めに持つとかぶせもしやすい
つまみ
ホイール横に指を置くとつまみ持ちになる。
幅広な感じが持ちやすいが手前を押すのはクリックがやや重い。
つかみ
持ちやすく母指球小指球が圧迫されずに手のひらでグリップできる。
両サイドは割とフラットな印象
おわり
非対称ですがチルトが緩いトップと台形的でない右サイドで、対称マウスユーザーでも使いやすい軽量・唯一無二形状のマウス。
懸念点はオプティカルスイッチ独特のクリック感と詰まった感じの右クリック、柔らかいフロント部分のシェル。
クリック感はオプティカルなりにクリスピーな感じで悪くない。
前の記事:Razer Viper Ultimate マウスレビュー
次の記事:Zowie FK2-B マウスレビュー
ところどころあれだけど形状好きなので使う。
kpuの幅が細いと感じていた。持つときに手が丸まりすぎると感じていた。
kpは幅が太くなって丁度良かった。縦に長く伸びることで傾斜が緩くなり手のわしづかみ感を緩くして持てるようになった。
roccatの光学スイッチはFPSであれば慣れれば結構使いやすいと感じる。
-
Razer Viper Ultimate マウスレビュー
フラグシップワイヤレスマウスLogicool G Pro Wirelessが発売されFPSに無線化の波がやってきました。
Logicoolに続いてRazerからより軽量な無線マウスViper Ultimateが発売されました。
今更ながら当時の軽量無線マウスの先駆けVPUをレビューしていきます。
FKクローンなマウスで同社Viper 、Viper 8Kが同形状です。
スペック
メーカー Razer ツイッター @RazerJP 製品ページ Viper Ultimate 接続 ワイヤレス 形状 左右対称 長さ 127 mm 幅 66.1 mm 高さ 38.5 mm(ソール 0.55mm抜き) 重さ 74.5 g スイッチ razerオプティカル センサー FOCUS+ LOD 1 mm(較正で1 mm未満) DPI 100-20k(50刻み) ポーリング 125/500/1000 Hz ソフトウェア Razer Synapse 3 形状
くびれの大きなFKクローンな形状。
上下


サイズ感
全長127 mmの中型マウスです。平べったくあまり大きさは感じませんがしっかりサイズがあります。
リア
尻の幅が66.1 mmあり中型マウスとしてはやや狭めで尻は長めに見えます。
中央
中央から5 mm程度フロント寄りに56.9 mmまでくびれています。FKに比べ深くくびれています。
キュッとくびれておりFKよりくびれに指を置いた時のフィット感があります。
フロント
59.9 mまで幅が広がっていきフロントでは丸まっています。
FKに比べよりフロントに幅が広がっていきます。FKに比べ側面のくびれとフロントの幅の差が大きいです。
逆台形度
逆台形度は3.6 mmと中程度でくびれ部からフロントまでほぼ一定となっています。
センサー位置
センサー位置は中央です。くびれはややフロント寄りでトップは中央から3 mm程度リア寄りとなっています。
横


トップ
TOPは中央から3 mm程度後方にあります。38.5 mmと低めで平べったい形状。
なだらかな尻
MB
クリック部分は指のガイドがある形状でMBは平べったい。
前後


FKぽい感じ。
特徴
- L 127 x W 56.9-66.1 x H 38.5 mm
- 全体的に平べったく、くびれは強いが指や手のひらの引っかかりがない。
- くびれが強くフロントが広がっているFKクローン
比較
中身
分解




ボトムのネジはT6特殊ねじです。
バッテリーとサイドスイッチがトップにつけられています。重心が上に寄りそう。
薄いシェルと見えない部分の肉抜きえ軽量化されている設計。
ビルドクオリティ
シェルは薄く肉抜きもされていて剛性は高くもないが普通の使用では物足りなく感じることもなさそう。悪くはない。
ホイール
kailh製のエンコーダで静かでしっかりノッチ感がある。
ホイールクリックは結構軽めだと思う。
クリック
回転するわけではないがMBに回転軸がありばねで下に押し下げられプレスを補助している。
LKタイプのオプティカルスイッチでメカニカルスイッチに比べ重めで返りが弱い。
結構個体差がありものによって硬さ等結構変わりそう。
サイドボタン
左右2つずつついている。出っ張りが小さくやや押しづらい。
ケーブル
付属のケーブルでないとケーブル根元の形状が合わず充電できないのでキーボードのケーブル外してさっと充電とかできない。
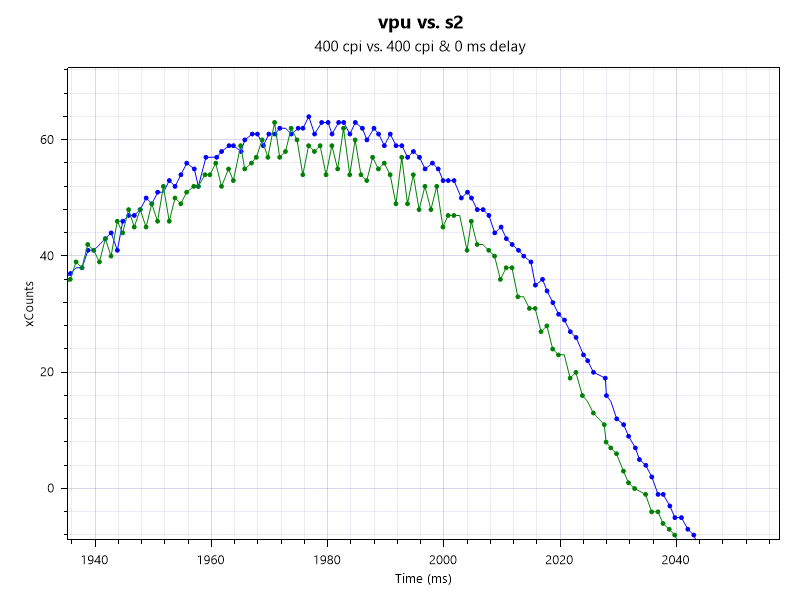
センサー
青がvpuです
入力遅延
有線マウスと比べ1.5~3 ms程度の入力遅延があります。FPSでは有線マウスにパフォーマンスが明らかに劣ります。
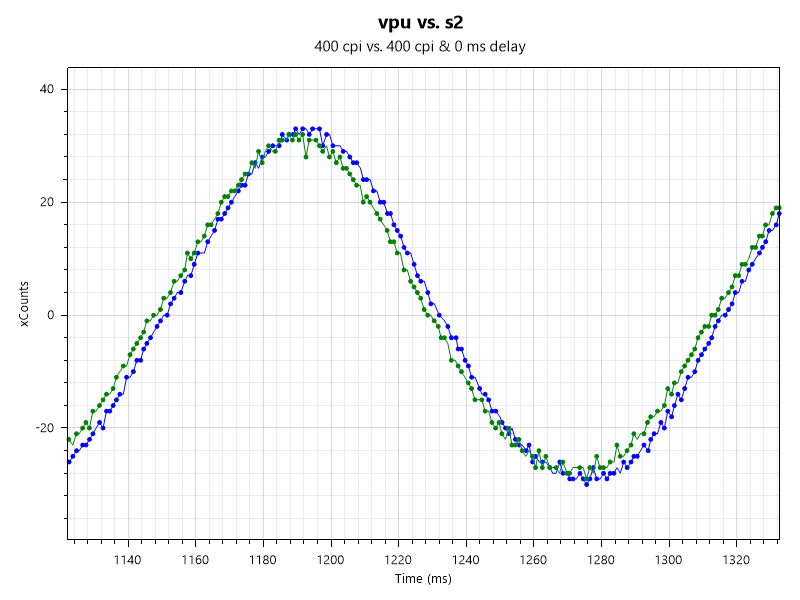
当時の対抗馬であるLogicool G ProWirelessと比べてみます。VPUの方が1 ms程度遅延が大きく波形がずれているのがわかります。pro wl恐るべし。
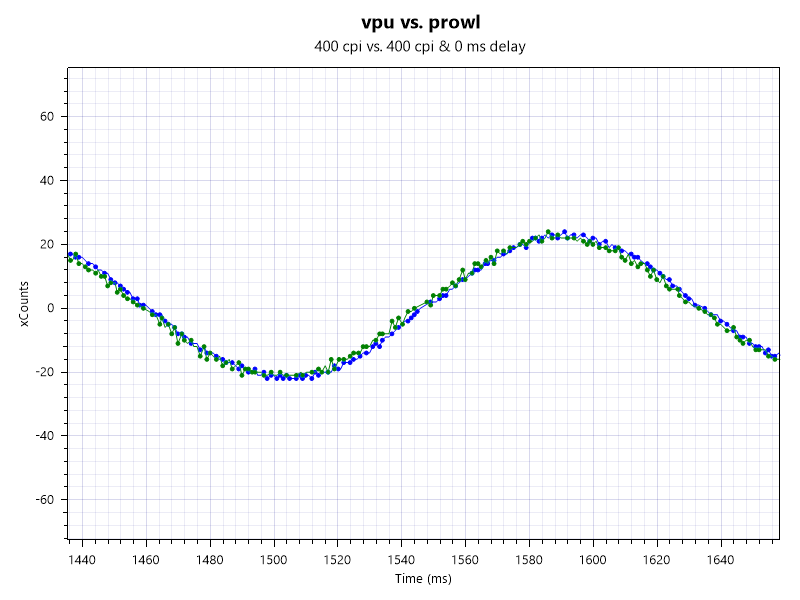
モーションシンク
3399カスタムのFOCUS+。ウリはモーションシンクというマウスの送信とpcの受信を同期させるという技術です。つまり画面とpcの垂直同期みたいなもんでしょうか。
同期ずれの分入力が早く正確になるというわけですね。
確かにジャギジャギが軽減されています。同期のずれ解消による遅延の削減はそもそも無線による遅延があるので今回は確認できませんでしたが期待できそうです。
LOD
LODは最低設定で1 mmちょっとと適切です。較正設定にすることで1 mm未満からLODを自由に設定できます。
ソフトウェア
Synapse 3で設定。G Hubもそうですが起動せずとも裏でプロセスが動いているのであまりいい気がしません。
- DPI:100-20k(50刻み、最大5ステージ、xy個別に設定可能)
- 125/500/1000 Hz
- LOD設定
- 背面含め9ボタンに自由度のあるボタン割り当てが可能。左クリックは固定。上下ホイールにも割り当て可能なマウスは珍しいと思う。
- ライティング設定可能
- オンボードメモリ(複数プロファイル)
グリップ
全体的に平べったくあまり指の引っかかりがない感じ。
フロントに幅が広がっていくのが好きな人はFKクローンの中でviperが合う。
重さ
74 g台と当時はpro wlよりも軽量なワイヤレスマウスであった。現在でもワイヤレスマウスの中で重い部類ではなく健闘している。
コーティング
細かい梨地な感じのマット。
サイドはラバーが貼ってある。滑り止め効果はそこまで。
つまみ
薄くなだらかな尻なのでつまみ持ちもしやすいがやや重さがあり引っかかりがない形状からグリップ力に欠ける。
つかみ
FKクローンなのだし合う。出っ張りが少ないので普通につかむのもわしづかみにするのも干渉せず合う。
かぶせ
特別フィット感はない。
おわり
当時ロジクールの後発として発売されたが無線技術はロジクールの方が勝っており有線と比べ1 msより大きい入力遅延がありFPSでの使用はパフォーマンスを発揮できない。
FOCUS+センサーのモーションシンクは一定の効果が見られ有線では同期ずれによる遅延を削減できるため有線モデルであるViper 8Kとかは遅延面で非常に強いかもしれない。オプティカルスイッチだし。
くびれが強くフロントに幅が広がっていくFKクローン形状。
懸念点はオプティカルスイッチの独特のクリック感と無線遅延。ホイール周りや他にはない同期センサーは結構いい感じ。
当時のワイヤレスマウスとしてはPROWLの形状が合わない人には買い。現在では最新のワイヤレスマウスには遅延面で弱くFPSでの使用は向いているとは言えない。やや高いがVPUより有線のVIPER 8Kを買う方が満足度が高いと思う。
前の記事:Vaxee Zygen NP-01 マウスレビュー
感想
もうだいぶ前のマウスなのであまり遅延があることに文句は言えないがまあrazerだしと期待していただけにちょっと驚いた。
個人的にラバーグリップは劣化するのであまり好きでなく滑り止め効果自体弱いので微妙。miniのように全面プラが好き。
このモーションシンクは面白いんじゃないかなと思います。
形状はFKベースなのでそこまで言うことはないですがキュッとした感じのくびれ部分は私はFK系にはそこまで合わない感じがしました。
VPUに限ったことじゃないですが充電部分が専用のケーブルじゃないとはまらない文化はやめてほしいです。無線のケーブルレスを快適と感じていませんし充電のために特定のケーブルを挿す方が煩わしく感じます。






































![[BF6]視野角と感度の設定について](https://tsuiha.com/wp-content/uploads/2025/10/image-36-3.jpg)
![[自キ]KS-33B Gateron LowProfile 3.0スイッチに希望はあるのか](https://tsuiha.com/wp-content/uploads/2025/09/IMG_3528.jpg)
![[自キ]チルトテントアルミケースな左手デバイス作る③修正](https://tsuiha.com/wp-content/uploads/2025/09/image-2.png)
![[自キ]チルトテントアルミケースな左手デバイス作る②ケース](https://tsuiha.com/wp-content/uploads/2025/08/image-26.jpg)
![[自キ]チルトテントアルミケースな左手デバイス作る①基板](https://tsuiha.com/wp-content/uploads/2025/08/image-24.jpg)


![[自キ]遊舎工房のレーザー加工サービス利用してみた](https://tsuiha.com/wp-content/uploads/2025/08/image-5-1.jpg)


![[自キ]磁気キーボードを作りたい。6週目](https://tsuiha.com/wp-content/uploads/2025/07/image-2.jpg)

![[自キ]磁気キーボードを作りたい。5週目](https://tsuiha.com/wp-content/uploads/2025/06/image-27.jpg)

![[自キ]磁気キーボードを作りたい。3週目](https://tsuiha.com/wp-content/uploads/2025/05/image-15-1.jpg)
![[自キ]磁気キーボードを作りたい。2週目](https://tsuiha.com/wp-content/uploads/2025/05/image-9.jpg)
![[自キ]磁気キーボードを作りたい。1週目](https://tsuiha.com/wp-content/uploads/2025/04/image-25-1.jpg)
![[自キ]50%オーソリニアのキーボード作った OSPREY59O](https://tsuiha.com/wp-content/uploads/2025/03/IMG_2343.jpg)






![[自作マウス]haste2基板を3Dモデルに起こした](https://tsuiha.com/wp-content/uploads/2025/01/image-10.jpg)

![[デスク]VESA拡張してモニターを増設した](https://tsuiha.com/wp-content/uploads/2025/01/IMG_2567.jpg)
![[デスク]充電ケーブルを天板裏に移動してすっきりした](https://tsuiha.com/wp-content/uploads/2025/01/IMG_2565.jpg)

![[自作マウス]マウスシェルモデリング その2](https://tsuiha.com/wp-content/uploads/2024/11/IMG_2288.jpg)

![[イヤホン]moondrop 水月雨 KadenzとKatoの雑話](https://tsuiha.com/wp-content/uploads/2024/11/IMG_2385.jpg)

![[オーディオ]ジェネリックER-4B化モジュールを作る②](https://tsuiha.com/wp-content/uploads/2024/08/er4switch1.jpg)
